Causal Directed Acylic Graphs
introduction
2024-08-06
Day 2 intro: Causal Directed Acyclic Graphs and Structural Causal Models
Today’s lectures
- introduce 1.5 new framework based on
- causal Directed Acyclic Graphs (DAGs)
- Structral Causal Models (SCMs)
- counterfactuals and Pearl’s Causal Hierarchy of questions
- lectures will follow Pearl’s book Causality Pearl (2009), specifically chapters 3 (DAGs) and 7 (SCMs)
Causal inference frameworks
What are they for?
Mathematical language to
- define causal quantities
- express assumptions
- derive how to estimate causal quantities
Causal inference frameworks
Why learn more than one?
- On day 1 we learned about the Potential Outcomes framework
- Defines causal effects in terms of (averages of) individual potential outcomes
- Estimation requires assumptions of (conditional) exchangeability and positivity / overlap and consistency
- There isn’t only 1 way to think about causality, find one that ‘clicks’
- Now we will learn another framework: Structural Causal Models and causal graphs
- causal relations and manipulations of variables
- Developed by different people initially - Judea Pearl, Peter Spirtes, Clark Glymour
- SCM approach is broader in that it can define more different types of causal questions
- Equivalence: given the same data and assumptions, get the same estimates
Lecture 1 & 2 topics
- motivating examples for DAGs
- what are DAGs
- causal inference with DAGs
- what is an intervention
- DAG-structures: confounding, mediation, colliders
- d-separation
- back-door criterion
Motivating examples
Example task: are hospital deliveries good for babies?



Example task: are hospital deliveries good for babies?
- You’re a data scientist in a children’s hospital
- Have data on
- delivery location (home or hospital)
- neonatal outcomes (good or bad)
- pregnancy risk (high or low)
- Question: do hospital deliveries result in better outcomes for babies?
Observed data
| location | |||
|---|---|---|---|
| home | hospital | ||
| risk | low | 648 / 720 = 90% | 19 / 20 = 95% |
| high | 40 / 80 = 50% | 144 / 180 = 80% |
- better outcomes for babies delivered in the hospital for both risk groups
Observed data
| location | |||
|---|---|---|---|
| home | hospital | ||
| risk | low | 648 / 720 = 90% | 19 / 20 = 95% |
| high | 40 / 80 = 50% | 144 / 180 = 80% | |
| marginal | 688 / 800 = 86% | 163 / 200 = 81.5% |
- better outcomes for babies delivered in the hospital for both risk groups
- but not better marginal (‘overall’)
- how is this possible?
- what is the correct way to estimate the effect of delivery location?
New question: hernia
- for a patient with a hernia, will they be able to walk sooner when recovering at home or when recovering in a hospital?
- observed data: location, recovery, bed-rest
Observed data 2
| location | |||
|---|---|---|---|
| home | hospital | ||
| bedrest | no | 648 / 720 = 90% | 19 / 20 = 95% |
| yes | 40 / 80 = 50% | 144 / 180 = 80% | |
| marginal | 688 / 800 = 86% | 163 / 200 = 81.5% |
- more bed rest in hospital
- what is the correct way to estimate the effect of location?
How to unravel this?
- we got two questions with exactly the same data
- in one example, ‘stratified analysis’ seemed best
- in the other example, ‘marginal analysis’ seemed best
- need a language to formalize this differentness
- with Directed Acyclic Graphs we can make our decision
Causal Directed Acyclic Graphs
diagram that represents our assumptions on causal relations
- nodes are variables
- arrows (directed edges) point from cause to effect

- when used to convey causal assumptions, DAGs are ‘causal’ DAGs1
Making DAGs for our examples:
The pregnancy DAG
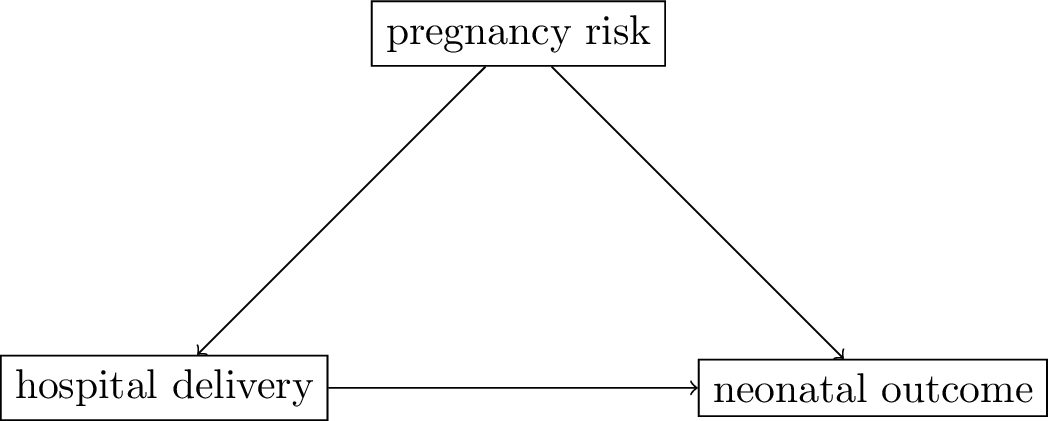
- assumptions:
- women with high risk of bad neonatal outcomes (
pregnancy risk) are referred to the hospital for delivery - hospital deliveries lead to better outcomes for babies as more emergency treatments possible
- both
pregnancy riskandhospital deliverycauseneonatal outcome
- women with high risk of bad neonatal outcomes (
- the other variable
pregnancy riskis a common cause of the treatment (hospital delivery) and the outcome (this is called a confounder)
Making DAGs for our examples:
The hernia DAG
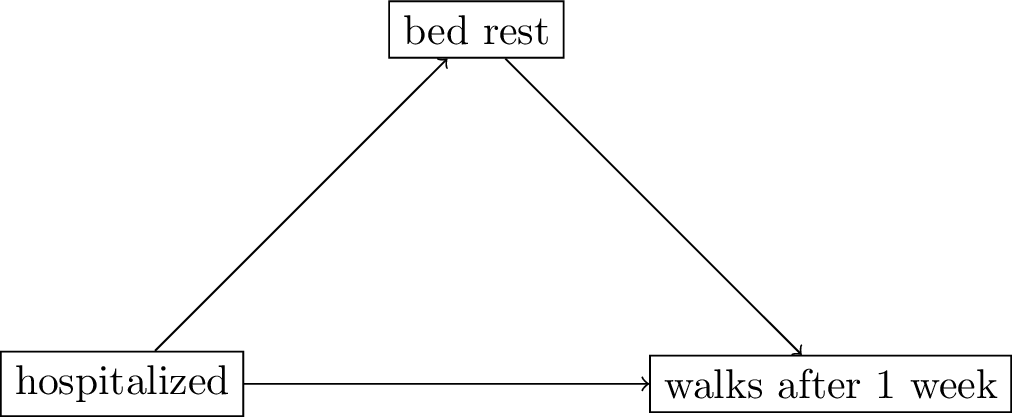
- assumptions:
- patients admitted to the hospital keep more
bed restthan those who remain at home bed restleads to lower recovery times thus less walking patients after 1 week
- patients admitted to the hospital keep more
- the other variable
bed restis a mediator between the treatment (hospitalized) and the outcome
Causal DAGs to the rescue
- the other variable was:
- a common cause (confounder) of the treatment and outcome in the pregnancy example
- a mediator between the treatment and the outcome in the hernia example
- using our background knowledge we could see something is different about these examples
- this insight prompted us to a different analysis
- next: ground this in causal theory and see implications for analysis
DAG definitions and properties
DAGs convey two types of assumptions:
causal direction and conditional independence
- causal direction: what causes what?


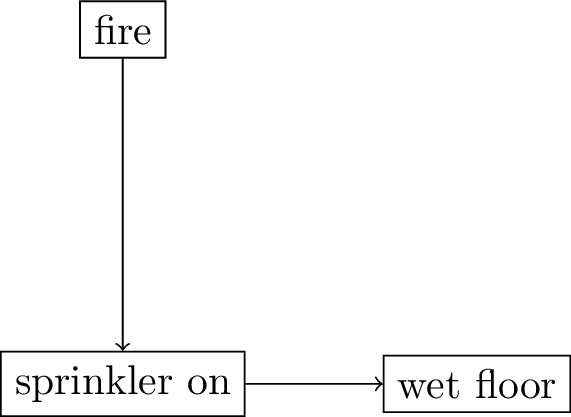
- read Figure 4 as
sprinkler onmay (or may not) causewet floorwet floorcannot causesprinkler on
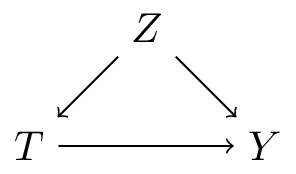
Basic DAG patterns: fork
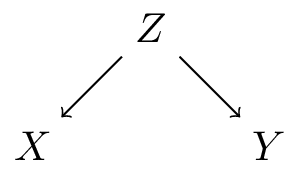
- \(Z\) causes both \(X\) and \(Y\) (common cause / confounder)
- \(Z\) = sun rises, \(X\) = rooster crows, \(Y\) = temperature rises
- \(X \mathrel{\not\!\perp} Y\) (i.e. \(X\) and \(Y\) are dependent)
- \(X \perp Y | Z\) (conditioning on the sun rising, the rooster crowing has no information on the temperature)
- \(Z \to X\) is a back-door: a path between \(X\) and \(Y\) that starts with an arrow into \(X\)
- typically want to adjust for \(Z\) (see later 6.4)
Basic DAG patterns: chain
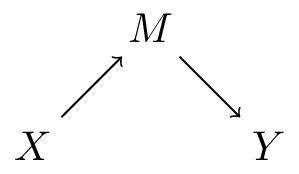
- \(M\) mediates effect of \(X\) on \(Y\)
- \(X\): student signs up for causal inference course, \(M\): student studies causal inference, \(Y\): student understands causal inference
- \(X \mathrel{\not\!\perp} Y\) (i.e. \(X\) and \(Y\) are dependent)
- \(X \perp Y | M\)
- typically do not want to adjust for \(M\) when estimating total effect of \(X\) on \(Y\)
Basic DAG patterns: collider
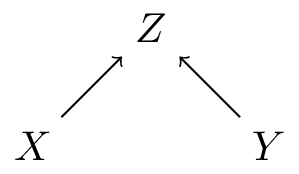
- \(X\) and \(Y\) both cause \(Z\)
- \(X \perp Y\) (but NOT when conditioning on \(Z\))
- often do not want to condition on \(Z\) as this induces a correlation between \(X\) and \(Y\)
Collider bias - Tinder

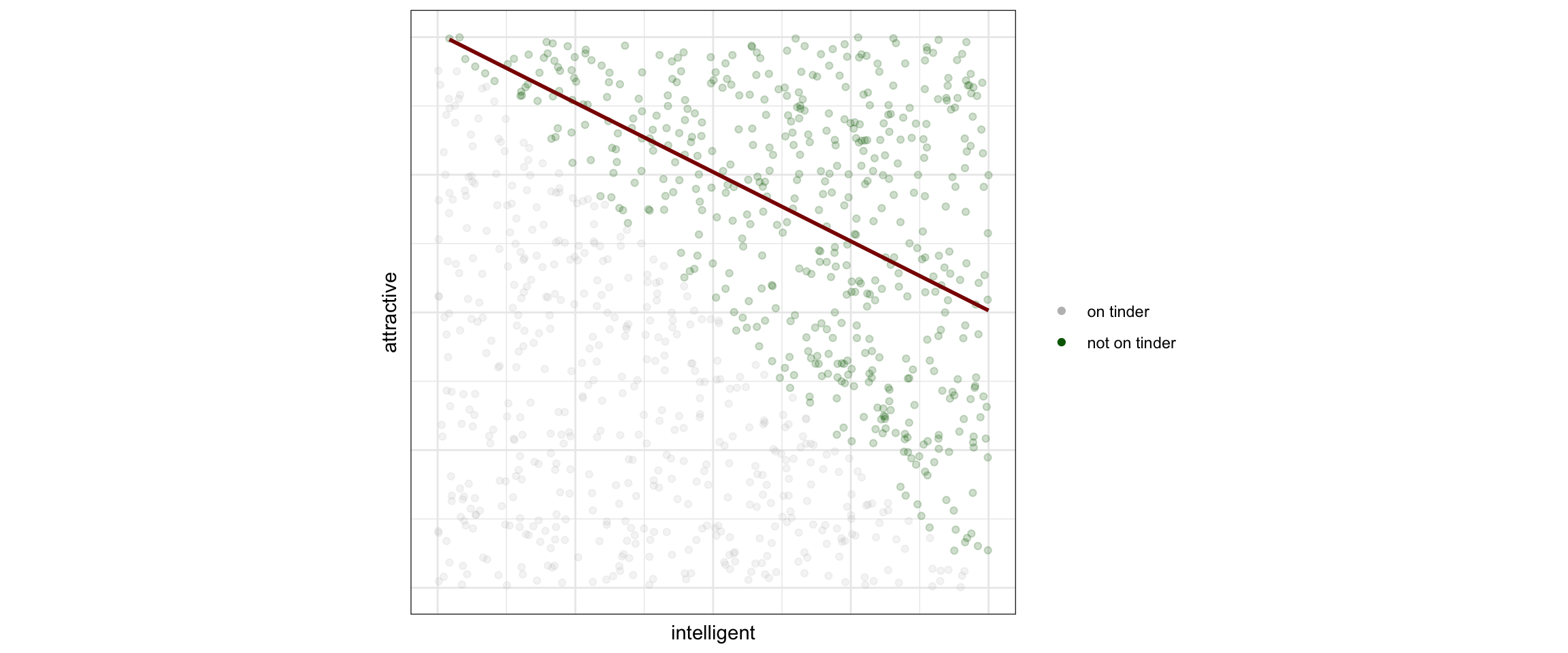
Conditioning on a collider creates dependence of its parents
- may not be too visible: doing an analysis in a selected subgroup is a form of (‘invisible’) conditioning
- e.g. when selecting only patients in the hospital
- being admitted to the hospital is a collider (has many different causes, e.g. traffic accident or fever)
- usually only one of these is the reason for hospital admission
- the causes for hospital admission now seem anti-correlated
DAGs convey two types of assumptions:
causal direction and conditional independence
- conditional indepence (e.g. exclusion of influence / information)
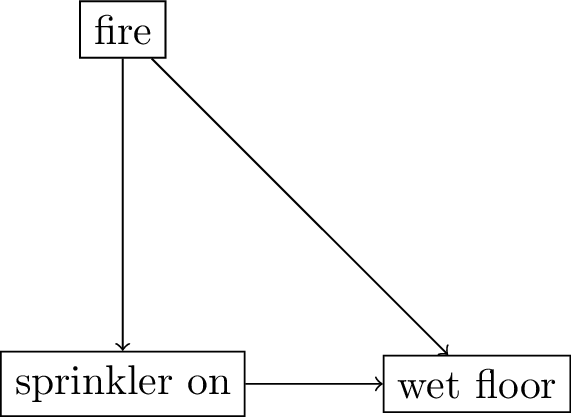
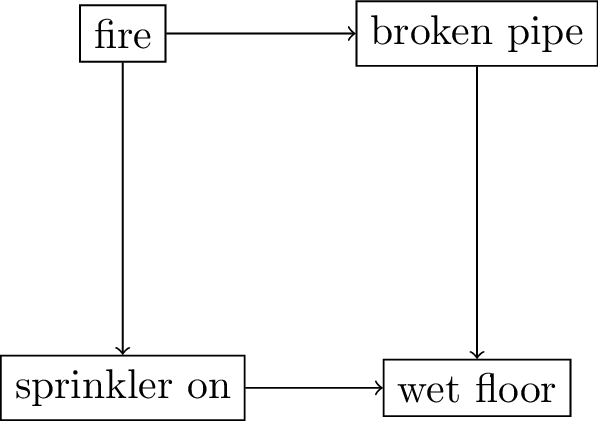
DAGs are ‘non-parametric’
They relay what variable ‘listens’ to what, but not in what way
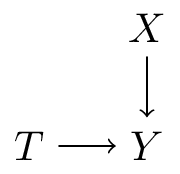
- this DAG says \(Y\) is a function of \(X,T\) and external noise \(U_Y\), or:
- \(Y = f_Y(X,T,U_Y)\)
- in the next lecture we’ll talk more about these ‘structural equations’
DAGs are ‘non-parametric’
They relay what variable ‘listens’ to what, but not in what way
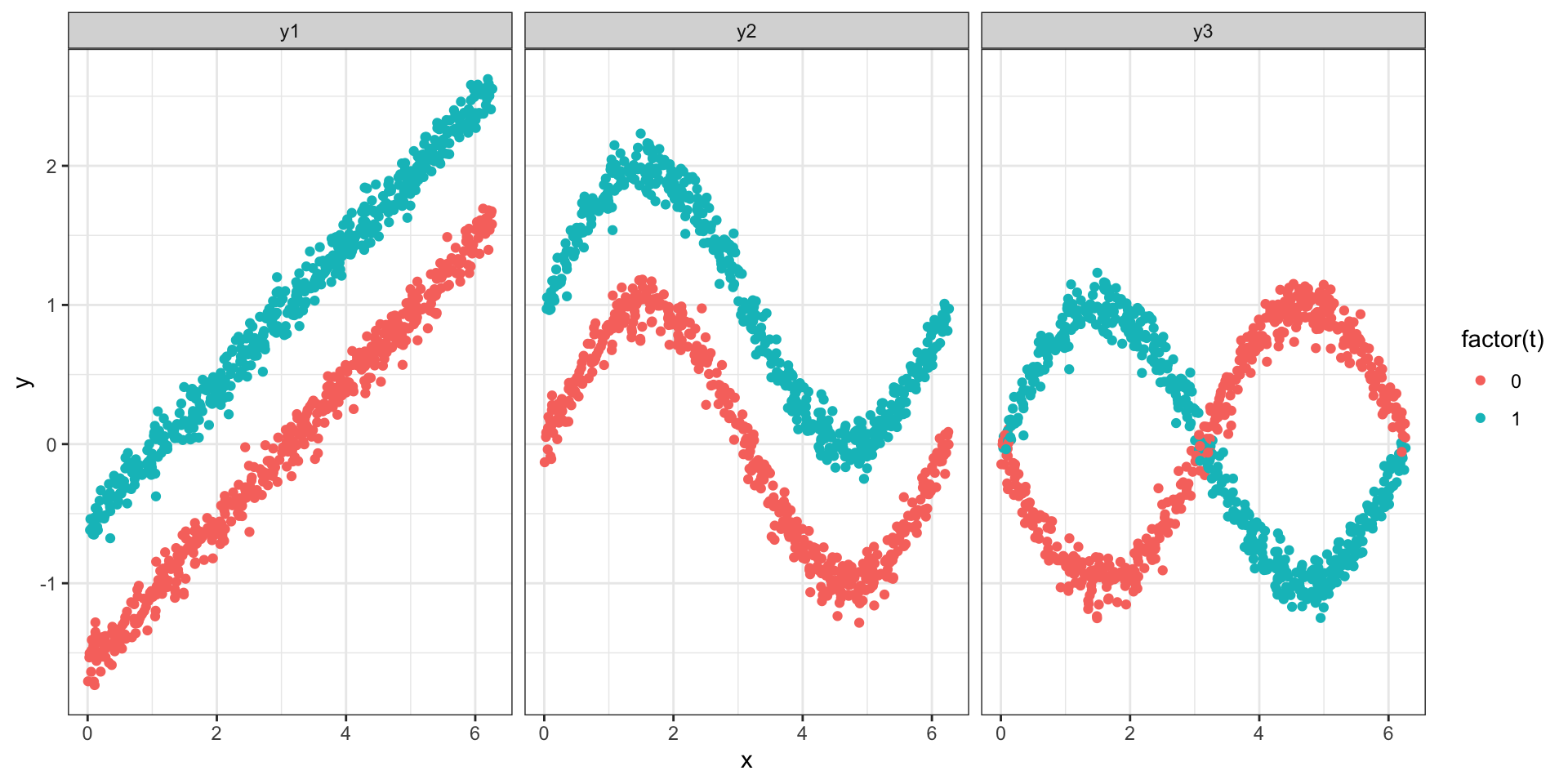
- \(Y = T + 0.5 (X - \pi) + \epsilon\) (linear)
- \(Y = T + \sin(X) + \epsilon\) (non-linear additive)
- \(Y = T * \sin(X) - (1-T) \sin(x) + \epsilon\) (non-linear + interaction)
Mini Quiz
Google Form https://bit.ly/dagquiz

From Directed Acyclic Graphs to causality
The DAG definition of an intervention
assume this is our DAG for a situation and we want to learn the effect \(T\) has on \(Y\)
- in the graph, intervening on variable \(T\) means removing all incoming arrows
- this assumes such a modular intervention is possible: i.e. leave everything else unaltered
- which means \(T\) does not listen to other variables anymore, but is set at a particular value, like in an experiment
- imagining this scenario requires a well-defined treatment variable (akin to consistency)
Intervention example: hospital deliveries

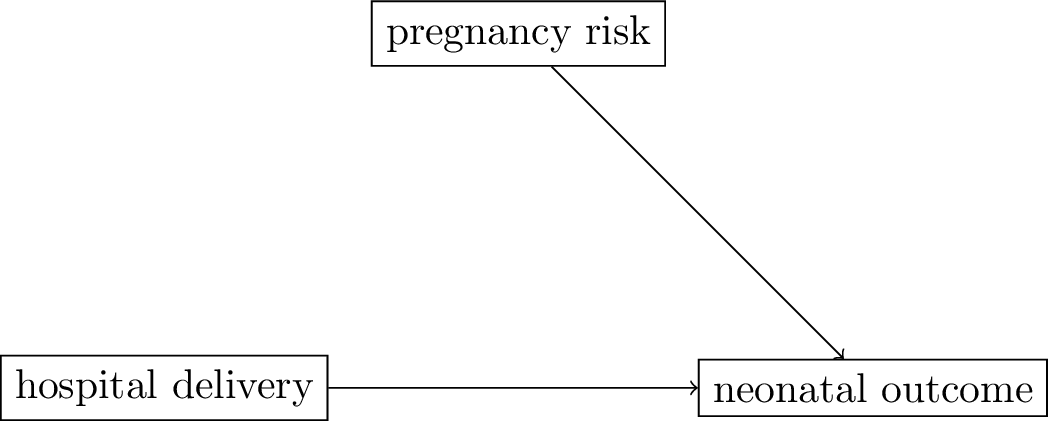
- this is called graph surgery because we cut all the arrows going to the treatment (hospital delivery)
From graph to data
- we now have a graphical definition of an intervention, how to map this onto data?
All we need is basic probability applied to the DAG
- product rule: \(P(A,B) = P(A|B)P(B)\)
- sum rule: \(P(A) = \sum_B P(A|B)P(B)\)
- total probability: \(P(A|C) = \sum_B P(A|B,C)P(B|C)\)
DAGs imply a causal factorization of the joint distribution
- assume these variables \(T\): treatment, \(Y\): outcome, \(Z\): ‘other’ variable
- the product rule allows us to write this joint in many (9) different factorizations, \(P(Y,T,Z)=\)
- \(P(Y|T,Z)P(T,Z)\)
- \(P(Z|T,Y)P(T,Y)\)
- \(P(Y|T,Z)P(T|Z)P(Z)\)
- …
- whereas all of these are correct, knowing the DAG, one of these is special: the causal factorization
DAGs imply a causal factorization of the joint distribution
\[\begin{align} P(Y,T,Z) &= P(Y|T,Z)P(T,Z) \\ &= P(Y|T,Z)P(T|Z)P(Z) \end{align}\]
- 2 times the product rule
- If this looks complicated: just follow the arrows, starting with variables with no incoming arrows
Intervention as graph surgery
Why is the causal factorization special?


\[\begin{align} P_{\text{obs}}(Y,T,Z) &= P(Y|T,Z)\color{red}{P(T|Z)}P(Z) \end{align}\]
\[\begin{align} P_{\text{int}}(Y,T,Z) &= P(Y|T,Z)\color{green}{P(T)}P(Z) \end{align}\]
- in the causal factorization, intervening on \(T\) means changing only one of the conditionals in the factorization, the others remain the same
- this is what is meant with a modular intervention
Intervention as graph surgery
Connection with probabilities
- the conditional distribution of \(Y\) given \(T\) is denoted as \(P(Y|T)\) (‘seeing’)
- the causal effect of \(T\) on \(Y\) is denoted \(P(Y|\text{do}(T))\), which is \(Y\) given \(T\) in the graph where all arrows coming in to \(T\) are removed (‘doing’)
- we compute this from the truncated factorization, which comes from the causal factorization by removing \(P(T|Z)\):
- causal factorization: \(P(Y|T,Z)P(T|Z)P(Z)\)
- truncated factorization: \(P(Y|T,Z)P(Z)\)
Intervention as graph surgery
Changed distribution


\[\begin{align} P_{\text{obs}}(Y,T,Z) &= P(Y|T,Z)\color{red}{P(T|Z)}P(Z) \\ P_{\text{obs}}(Y|T) &= \sum_{z} P(Y|T,Z=z)P(Z=z|T) \end{align}\]
\[\begin{align} P_{\text{int}}(Y,T,Z) &= P(Y|T,Z)\color{green}{P(T)}P(Z) \\ P_{\text{int}}(Y|T) &= \sum_{z} P(Y|T,Z=z)P(Z=z|T) \\ &\class{fragment}{= \sum_{z} P(Y|T,Z=z)\color{green}{P(Z)}} \\ &\class{fragment}{= P(Y|\text{do}(T))} \end{align}\]
Intervention as graph surgery - changed distribution

\[P_{\text{obs}}(Y|T) = \sum_{z} P(Y|T,Z=z)\color{red}{P(Z=z|T)}\]

\[P_{\text{int}}(Y|T) = \sum_{z} P(Y|T,Z=z)\color{green}{P(Z=z)} \qquad(1)\]
- in \(P_{\text{obs}}\), \(P(Z|T) \color{red}{\neq} P(Z)\)
- in \(P_{\text{int}}\), \(P(Z|T) \color{green}{=} P(Z)\)
- thereby \(P_{\text{obs}}(Y|T) \neq P_{\text{int}}(P(Y|T)) = P(Y|\text{do}(T))\)
- seeing is not doing
- looking at Equation 1, we can compute these from \(P_{\text{obs}}\)! (this is what is called an estimand)
Back to example 1
Seeing

| location | |||
|---|---|---|---|
| home | hospital | ||
| risk | low | 648 / 720 = 90% | 19 / 20 = 95% |
| high | 40 / 80 = 50% | 144 / 180 = 80% | |
| marginal | 688 / 800 = 86% | 163 / 200 = 81.5% |
- seeing: \(P(\text{outcome}|\text{location}) = \sum_{\text{risk}} P(\text{outcome}|\text{location},\text{risk})P(\text{risk}|\text{location})\)
- \(P(\text{risk}=\text{low} | \text{location} = \text{hospital})=10\%\)
- \(P(\text{risk}=\text{low} | \text{location} = \text{home})=90\%\)
\[\begin{align} P(\text{outcome}|\text{location} = \text{hospital}) &= 95 * 0.1 + 80 * 0.9 = 81.5\% \\ P(\text{outcome}|\text{location} = \text{home}) &= 90 * 0.9 + 50 * 0.1 = 86\% \end{align}\]
- conclusion: deliveries in the hospital had worse neonatal outcomes
Back to example 1

| location | |||
|---|---|---|---|
| home | hospital | ||
| risk | low | 648 / 720 = 90% | 19 / 20 = 95% |
| high | 40 / 80 = 50% | 144 / 180 = 80% | |
| marginal | 688 / 800 = 86% | 163 / 200 = 81.5% |
- estimand: \(P(\text{outcome}|\text{do}(\text{location})) = \sum_{\text{risk}} P(\text{outcome}|\text{location},\text{risk})P(\text{risk})\)
- \(P(\text{risk}=\text{low})=74\%\)
\[\begin{align} P(\text{outcome}|\text{do}(\text{hospital})) &= 95 * 0.74 + 80 * 0.26 = 91.1\% \\ P(\text{outcome}|\text{do}(\text{home})) &= 90 * 0.74 + 50 * 0.26 = 79.6\% \end{align}\]
- conclusion: sending all deliveries to the hospital leads to better neonatal outcomes
Back to example 2

- removing all arrows going in to \(T\) results in the same DAG
- so \(P(Y|T) = P(Y|\text{do}(T))\)
- i.e. use the marginals
The gist of observational causal inference
is to take data we have to make inferences about data from a different distribution (i.e. the intervened-on distribution)
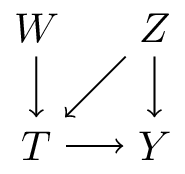
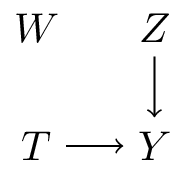
- causal inference frameworks provide a language to express assumptions
- based on these assumptions, the framework tells us whether such an inference is possible
- this is often referred to as is the effect identified
- and provide formula(s) for how to do so based on the observed data distribution (estimand(s))
- (one could say this is essentially assumption-based extrapolation, some researchers think this entire enterprise is anti-scientific)
- not yet said: how to do statistical inference to estimate the estimand (much can still go wrong here)
- can also be part of identification, see the following lecture on SCMs
Beyond toy examples: d-separation and back-door criterion
When life gets complicated / real
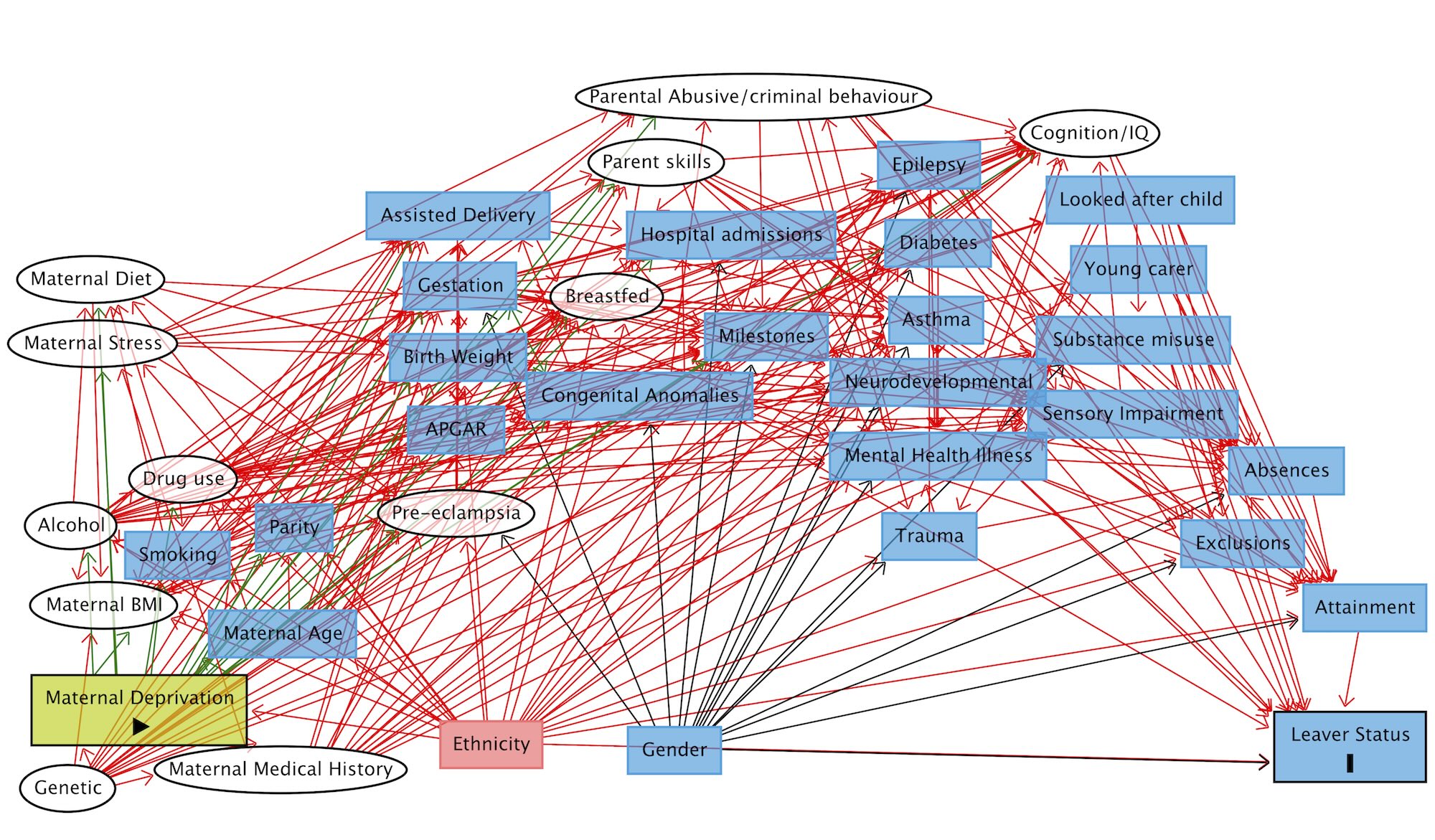
Bogie, James; Fleming, Michael; Cullen, Breda; Mackay, Daniel; Pell, Jill P. (2021). Full directed acyclic graph.. PLOS ONE. Figure. https://doi.org/10.1371/journal.pone.0249258.s003
d-separation (directional-separation)
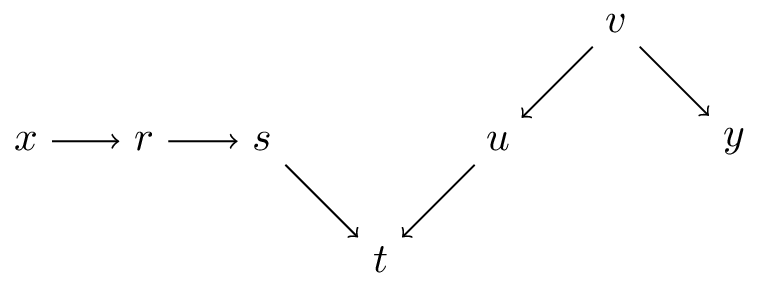
paths
- a path is a set of nodes connected by edges (\(x \ldots y\))
- a directed-path is a path with a constant direction (\(x \dots t\))
- an unblocked-path is a path without a collider (\(t \ldots y\))
- a blocked-path is a path with a collider (\(s,t, u\))
- d(irectional)-separation of \(x,y\) means there is no unblocked path between them
d-separation when conditioning
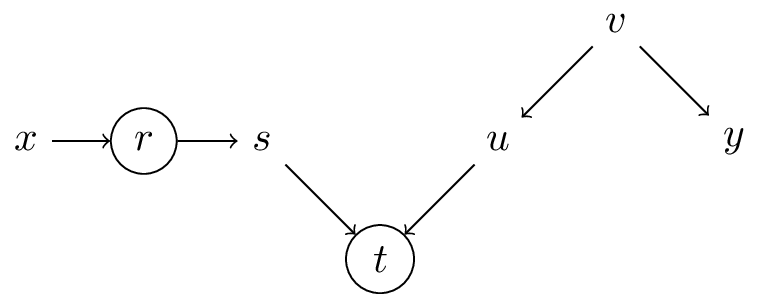
paths with conditioning variables \(r\), \(t\)
- conditioning on variable:
- when variable is a collider: opens a path (\(t\) opens \(s,t,u\) etc.)
- otherwise: blocks a path (e.g. \(r\) blocks \(x,r,s\))
- conditioning set \(Z=\{r,t\}\): set of conditioning variables
The back-door criterion and adjustment
Definition 3.3.1 (Back-Door) (for pairs of variables)
A set of variables \(Z\) satisfies the back-door criterion relative to an ordered pair of variables \((X,Y)\) in a DAG if:
- no node in \(Z\) is a descendant of \(X\) (e.g. mediators)
- \(Z\) blocks every path between \(X\) and \(Y\) that contains an arrow into \(X\)
Theorem 3.2.2 (Back-Door Adjustment)
If a set of variables \(Z\) satisfies the back-door criterion relative to \((X,Y)\), then the causal effect of \(X\) on \(Y\) is identifiable and is given by the formula
\[P(y|\text{do}(x)) = \sum_z P(y|x,z)P(z) \qquad(2)\]
Did we see this equation before?
- Yes! When computing the effect of hospital deliveries on neonatal outcomes Equation 1
- DAGs tell us what to adjust for
- automatic algorithms tell use whether an estimand exists and what it is
- several point-and-click websites for making DAGs that implement these algorithms:
How about positivity
backdoor adjustment with \(z\) requires computing \(P(y|x,z)\)
by the product rule:
\[P(y|x,z) = \frac{P(y,x,z)}{P(x,z)}\]
this division is only defined when \(P(x,z) > 0\)
which is the same as the positivity assumption from Day 1 in Potential Outcomes
References

Wouter van Amsterdam — WvanAmsterdam — vanamsterdam.github.io