A causal viewpoint on prediction model performance under changes in case-mix

Methods meeting at the Julius Center, UMC Utrecht

Wouter van Amsterdam, MD PhD

2024-11-25

Table of contents

• Recap of performance metrics: discrimination and calibration
• A causal description of shifts in case-mix
• Illustrative simulation and empirical validation

Motivation

• clinicians use prediction models for medical decisions, e.g.
  • making a diagnosis
  • estimating a patients prognosis
  • triaging
  • treatment decisions
• these prediction models need reliable performance
• issue: potential substantive difference between last evaluation and current use

Change in setting

What can we expect from the model’s performance (if anything) in the new setting?

model trained / evaluated in tertiary care hospital

model used in GP setting

This paper / talk

• recap performance: discrimination, calibration
• look at the causal direction of the prediction:
  • are we predicting an effect based on its causes (e.g. heart attack, based on cholesterol and age)
  • are we predicting a cause based on its effects (infer presence of CVA based on neurological symptoms)
• define shift in case-mix as a change in the marginal distribution of the cause variable
• conclude that in theory:
  • for prognosis models: expect stable calibration, not discrimination
  • for diagnosis models: expect stable discrimination, not calibration
• illustrate with simulation
• evaluate on 2030+ prediction model evaluations

Recap of performance metrics: discrimination and calibration

Discrimination: sensitivity, specificity, AUC

• prediction model \(f: X \to [0,1]\) (i.e. predicted probability, e.g. logistic regression)
• take a threshold \(\tau\), such that \(f(x) > \tau\) is a positive prediction
• tabulate predictions vs outcomes

		outcome
		1	0
prediction	1	true positives	false positives
	0	false negatives	true negatives

Discrimination: sensitivity, specificity

		outcome
		1	0
prediction	1	true positives	false positives
	0	false negatives	true negatives
		sensitivity: TP / (TP+FN)	specificity: TN / (TN+FP)

• sensitivity: \(P(X=1 | Y=1)\), specificity: \(P(X=0 | Y=0)\)

• note: sensitivity only requires data from the column of postive cases (i.e. \(Y=1\)), and specificity on negatives

• event-rate: fraction of \(Y=1\) of total cases

• in theory discrimination is event-rate independent (Hond 2023)

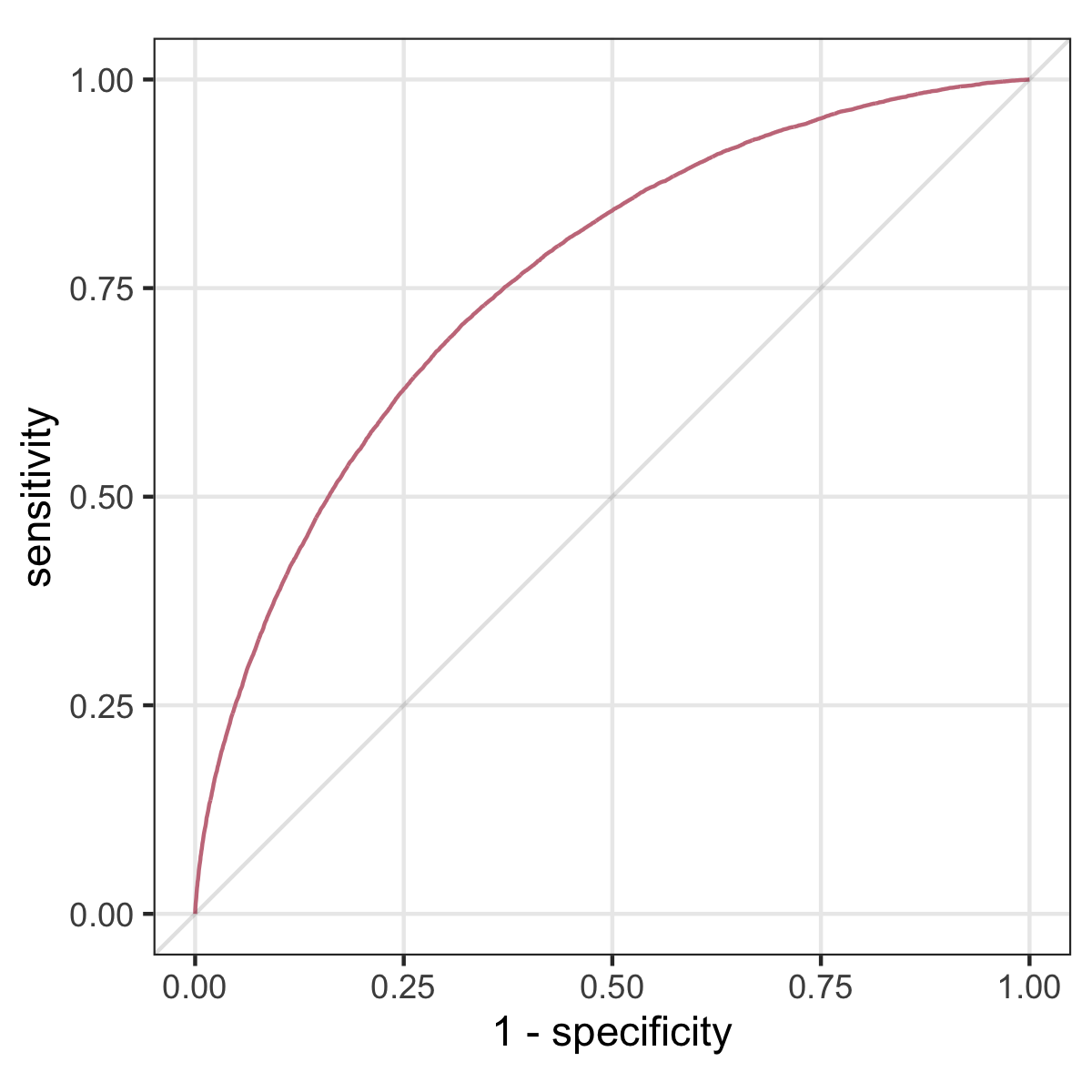
Discrimination: ROC curve and AUC

if we vary the threshold \(0 \leq \tau \leq 1\), we get a ROC curve, and the AUC is the area under this curve

Calibration

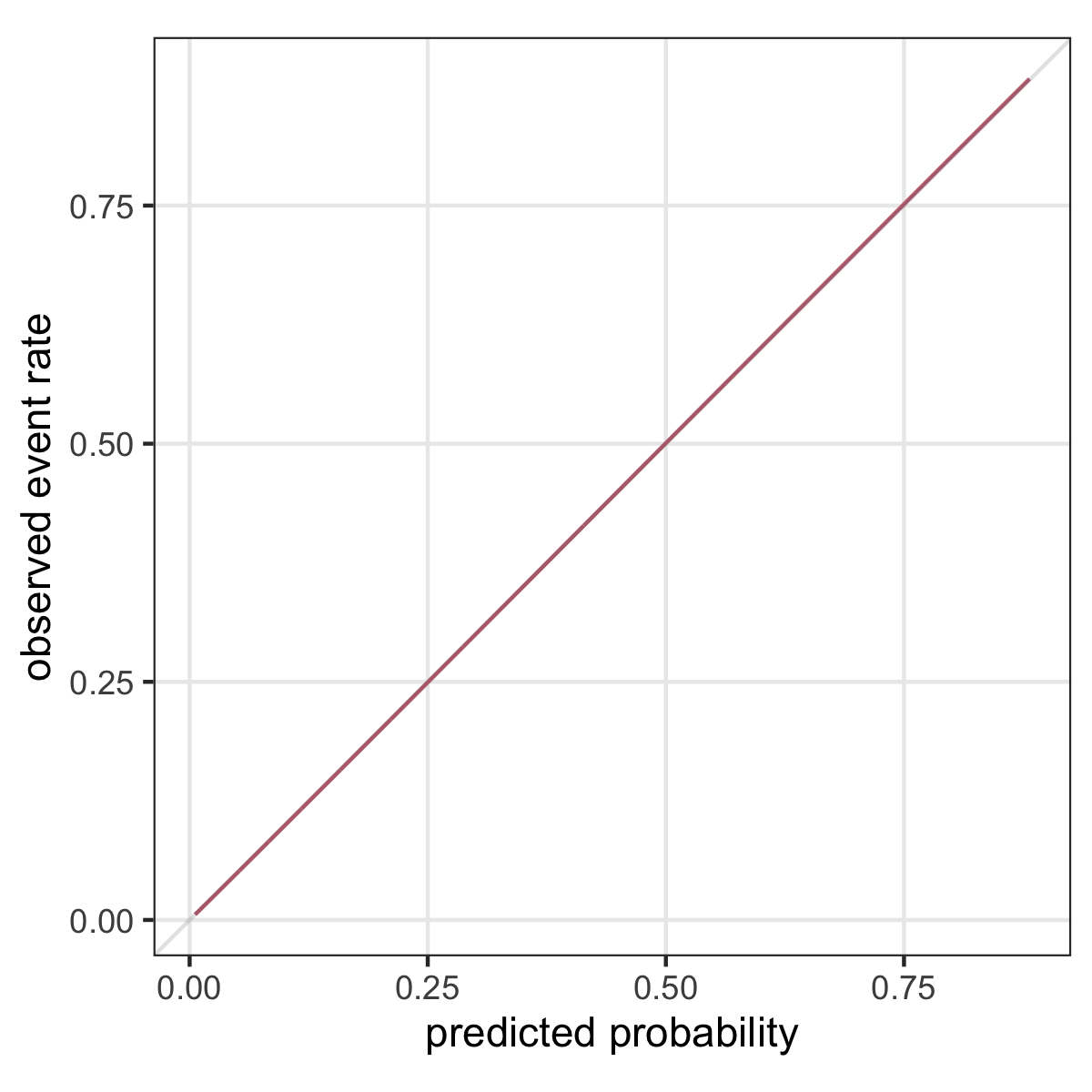
“A model is said to be well calibrated if for every 100 patients given a risk of x%, close to x have the event.” (Van Calster and Vickers 2015)

population

subgroup where \(f(x)=10\)%

event rate in said subgroup is 10%: \(p(Y=1|f(x)=10\%) = 10\%\)

Calibration plot

\(p(Y=1|X)\) versus \(f(x)\)

calibration

calibration-plot

Performance metrics summary

• discrimination: function of \(P(X|Y)\) (features given outcome)
• calibration: function of \(P(Y|X)\) (outcome given features)

A causal description of shifts in case-mix

Where does the association come from?

In prediction, we have features \(X\) and outcome \(Y\) and model \(Y|X\)

1. \(X\) causes \(Y\): often in prognosis (\(Y\): heart-attack, \(X\): cholesterol and age)

2. \(Y\) causes \(X\): often in diagnosis (CVA, based on neurological symptoms)

3. \(Z\) causes both \(X\) and \(Y\): confounding (yellow fingers predict lung cancer)

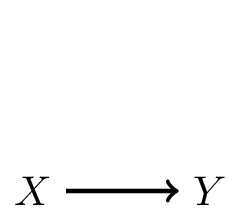
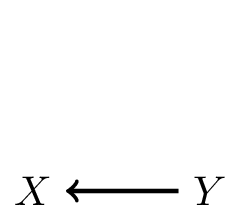
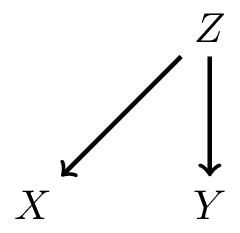
Defining a shift in case-mix

Define a shift in case-mix a change in the marginal distribution of the cause variable, e.g.

• filter on risk factors (pregancies with type 1 diabetes in hospital)
• filter on outcome risk (send patients with neurological symptoms to CVA center)
• denote environment as variable \(E\):

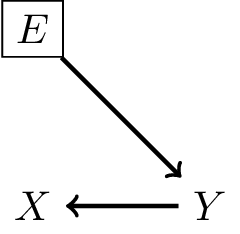
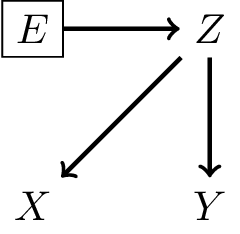
What does this definition imply?

• \(P(Y|X,E) = P(Y|X)\)
  • in words: \(P(Y|X)\) is transportable across environments
  • because there is no arrow from \(E\) to \(Y\), \(X\) blocks effect of \(E\) on \(Y\)
• \(P(X|Y,E) \neq P(X|Y)\)
  • in words: \(P(X|Y)\) is not transportable across environments
• implication for causal (prognosis) prediction:
  • calibration is functional of \(P(Y|X)\), thus stable
  • discrimination is functional of \(P(X|Y)\), thus not stable
• for anti-causal (diagnosis) prediction: the reverse
• main result: discrimination or calibration may be preserved under changes in case-mix, but never both

Why define a shift in case-mix this way?

1. cause is temporally prior to effect, filtering at least on cause may be likely in many settings
2. filtering on both: anything goes, cannot say anything about expected performance based on graphical information

Illustrative simulation and empirical validation

Simulation setup

\[\begin{align*} \label{eq:dgm-prognosis} \text{prognosis:} & & \text{diagnosis:} & \\ P_y &\sim \text{Beta}(\alpha_e,\beta_e) & y &\sim \text{Bernouli}(P_e) \\ x &= \text{logit}(P_y) & x &\sim N(y, 1) \\ y &\sim \text{Bernoulli}(P_y) & & \end{align*}\]

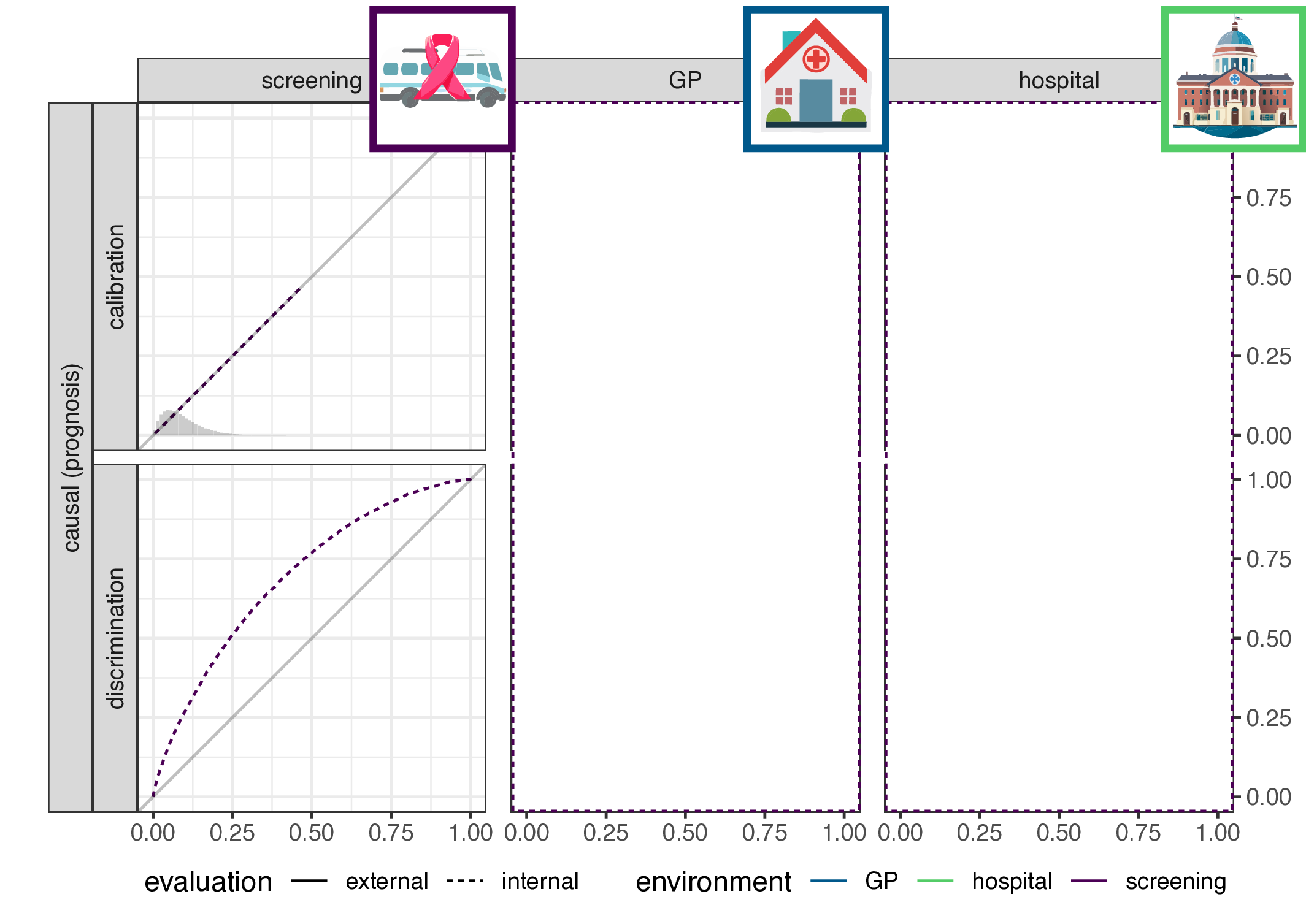
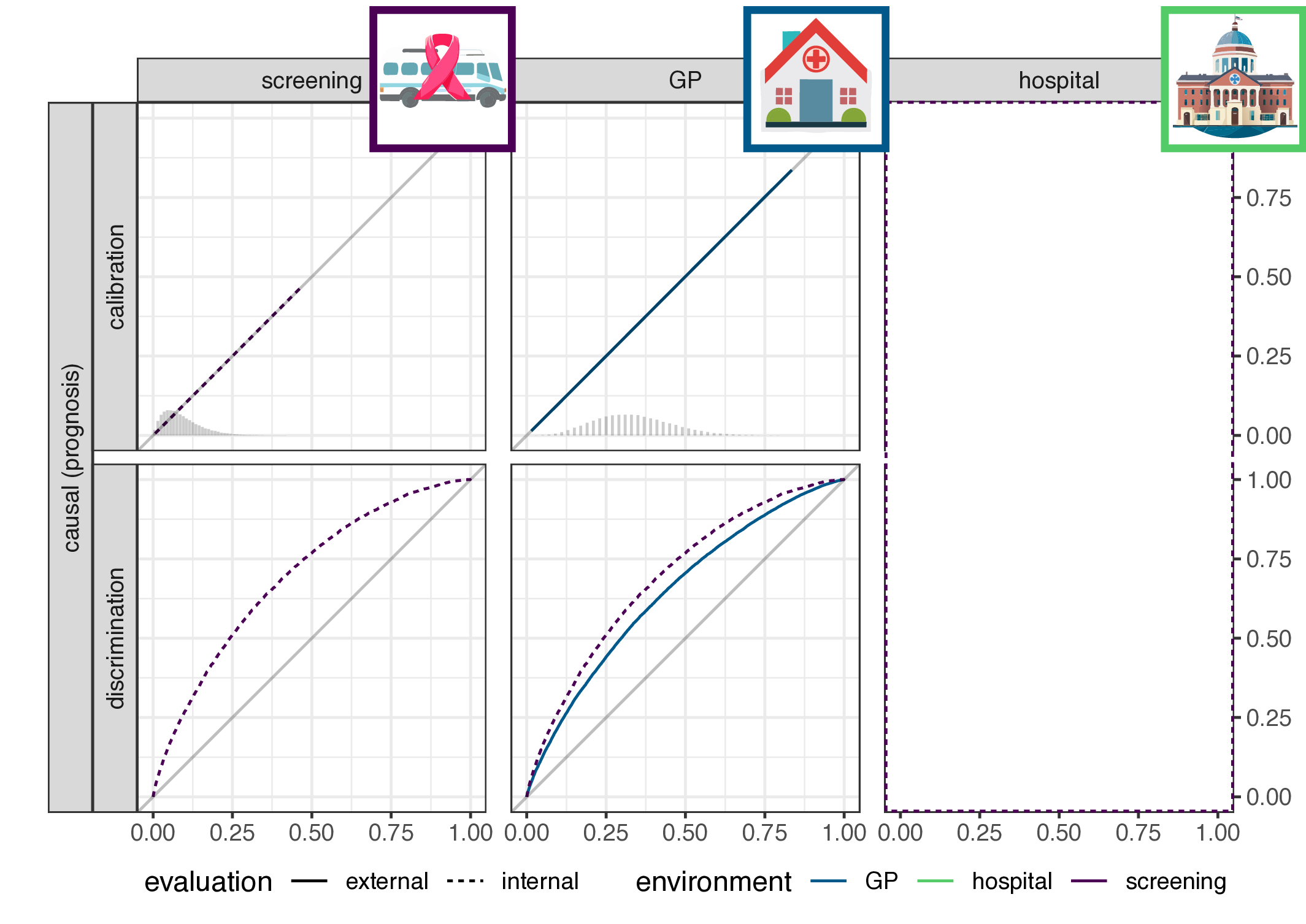
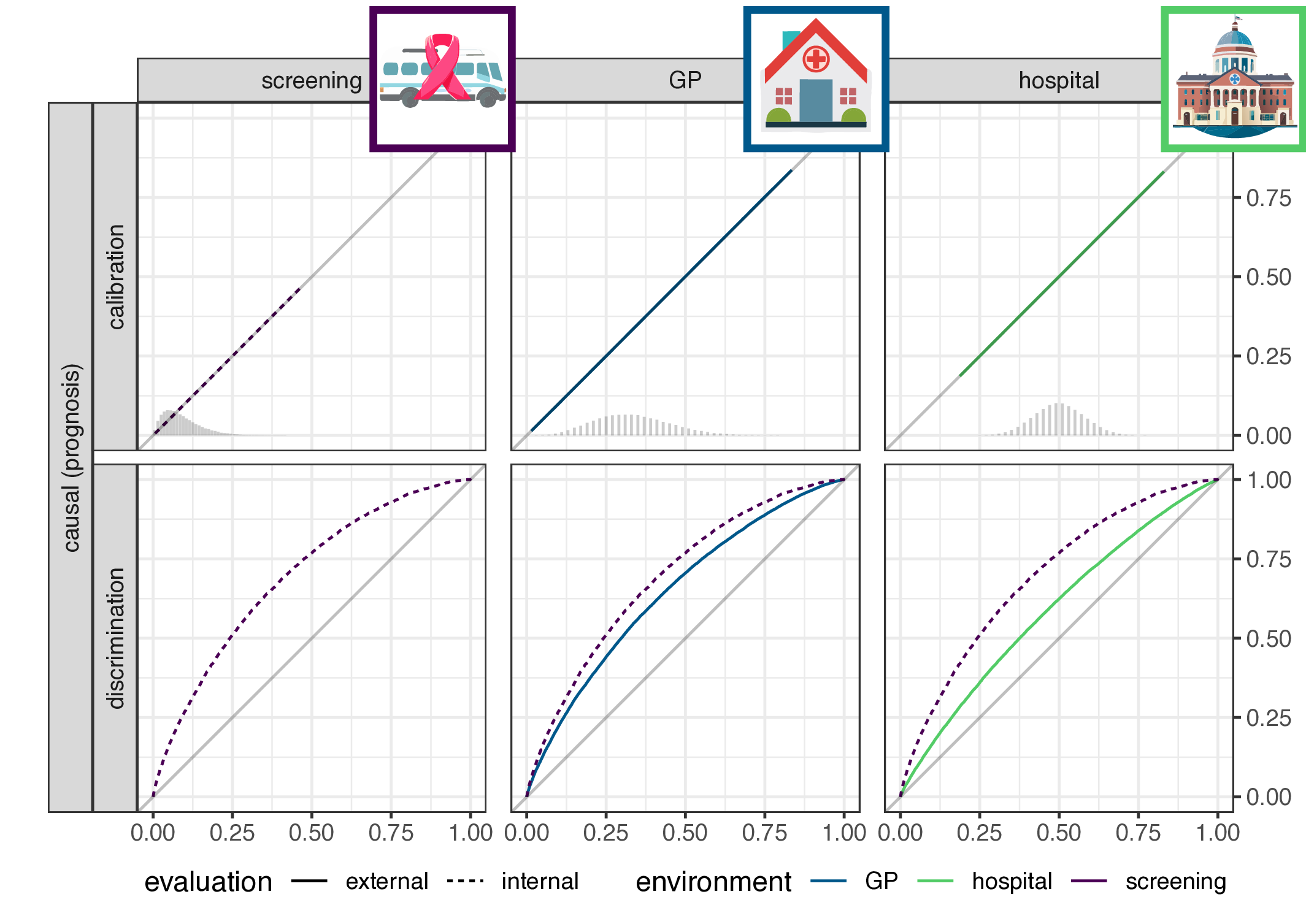
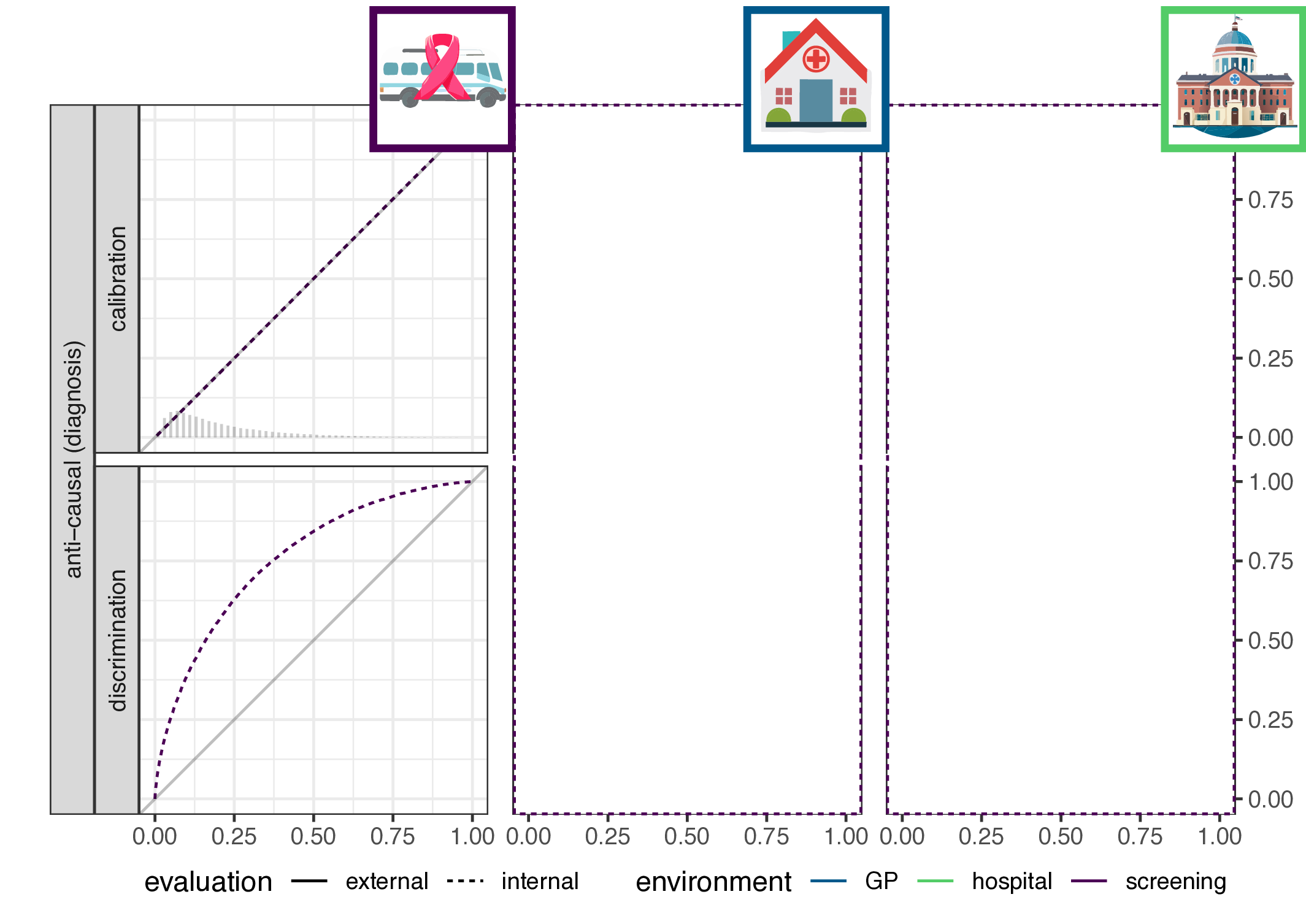
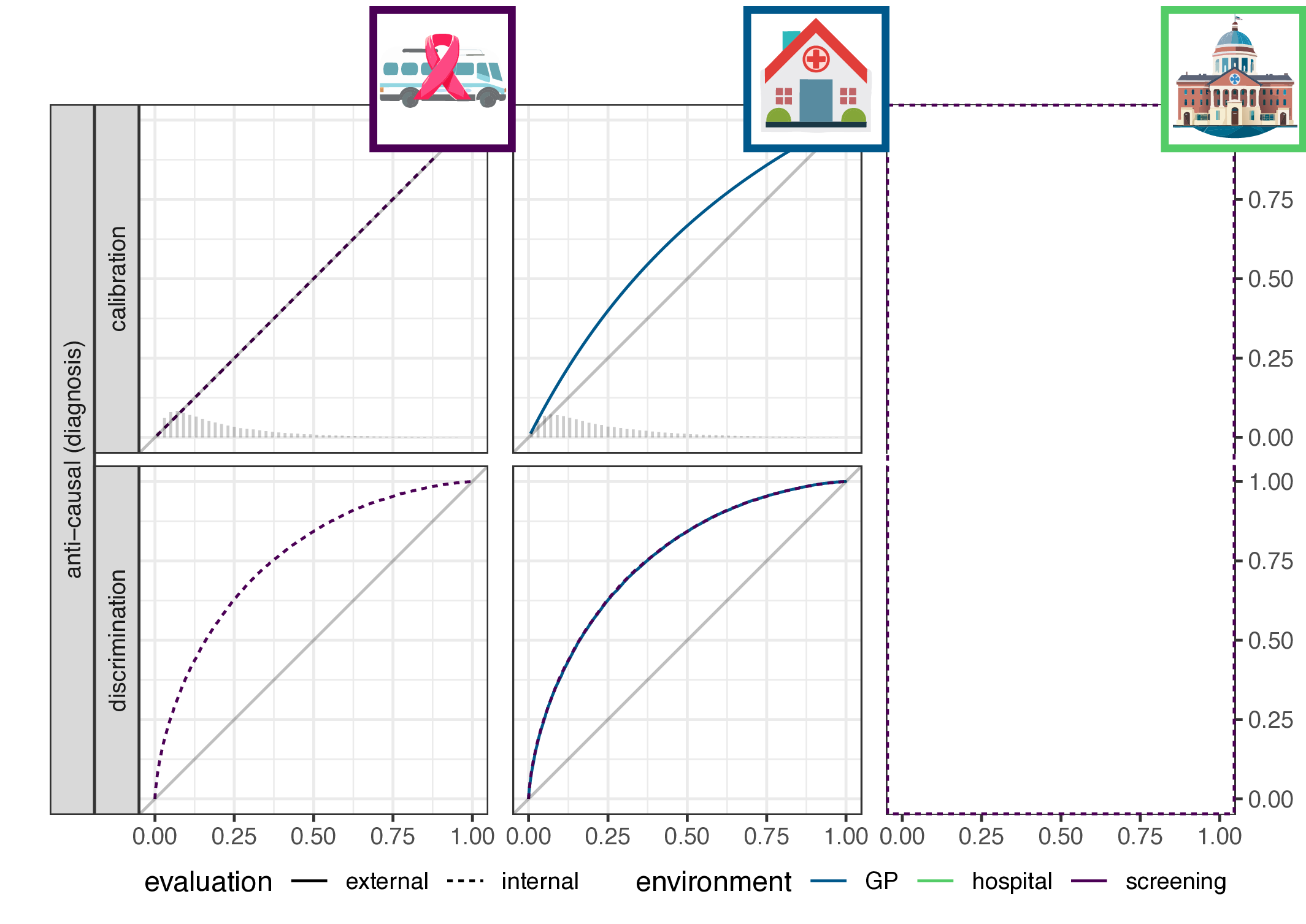
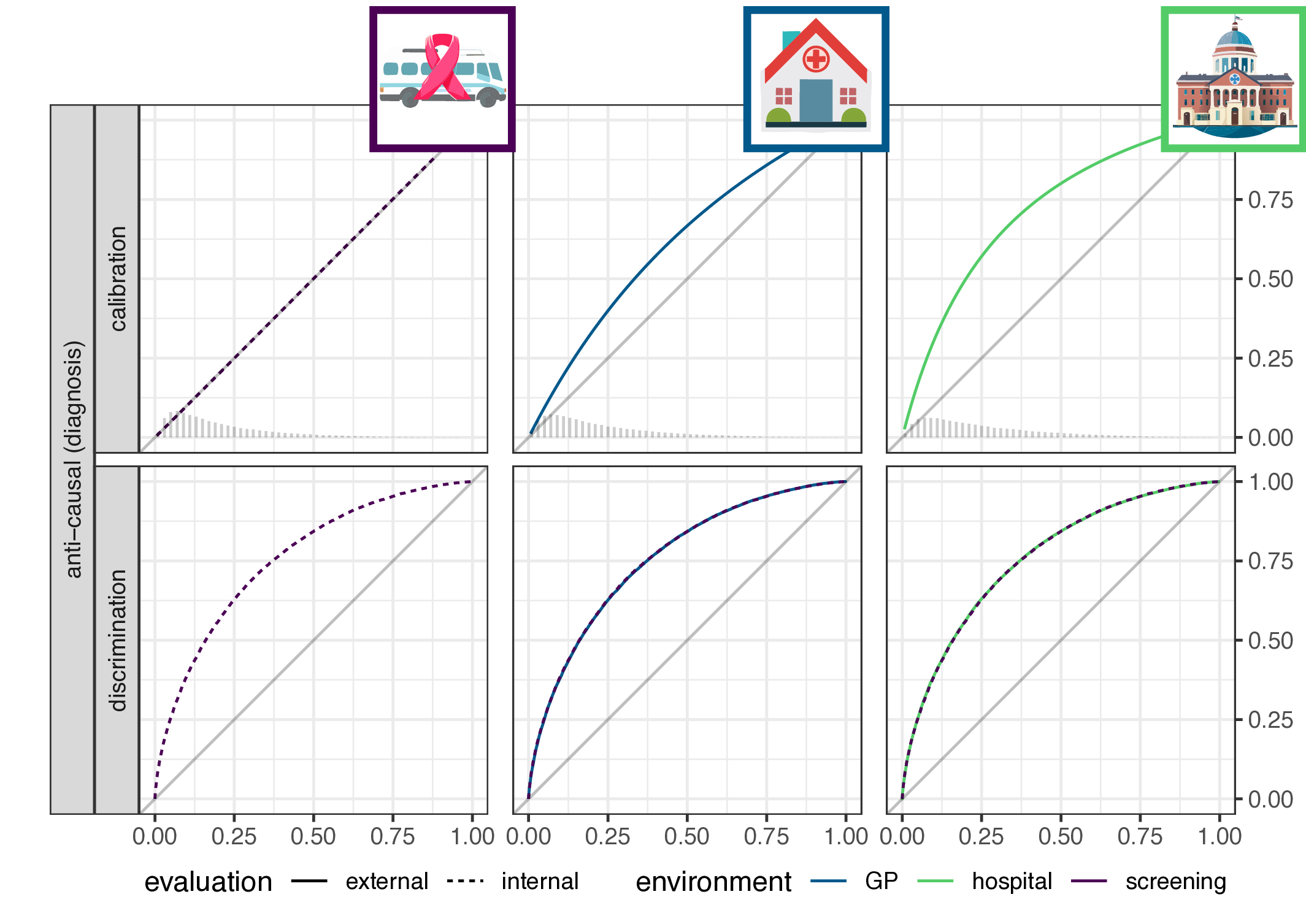
Empirical validation

• a study of 2030+ evaluations of 1300+ prediction models (Wessler et al. 2021)

• registry: all data available with only 4000 clicks
• solution: scrape the website

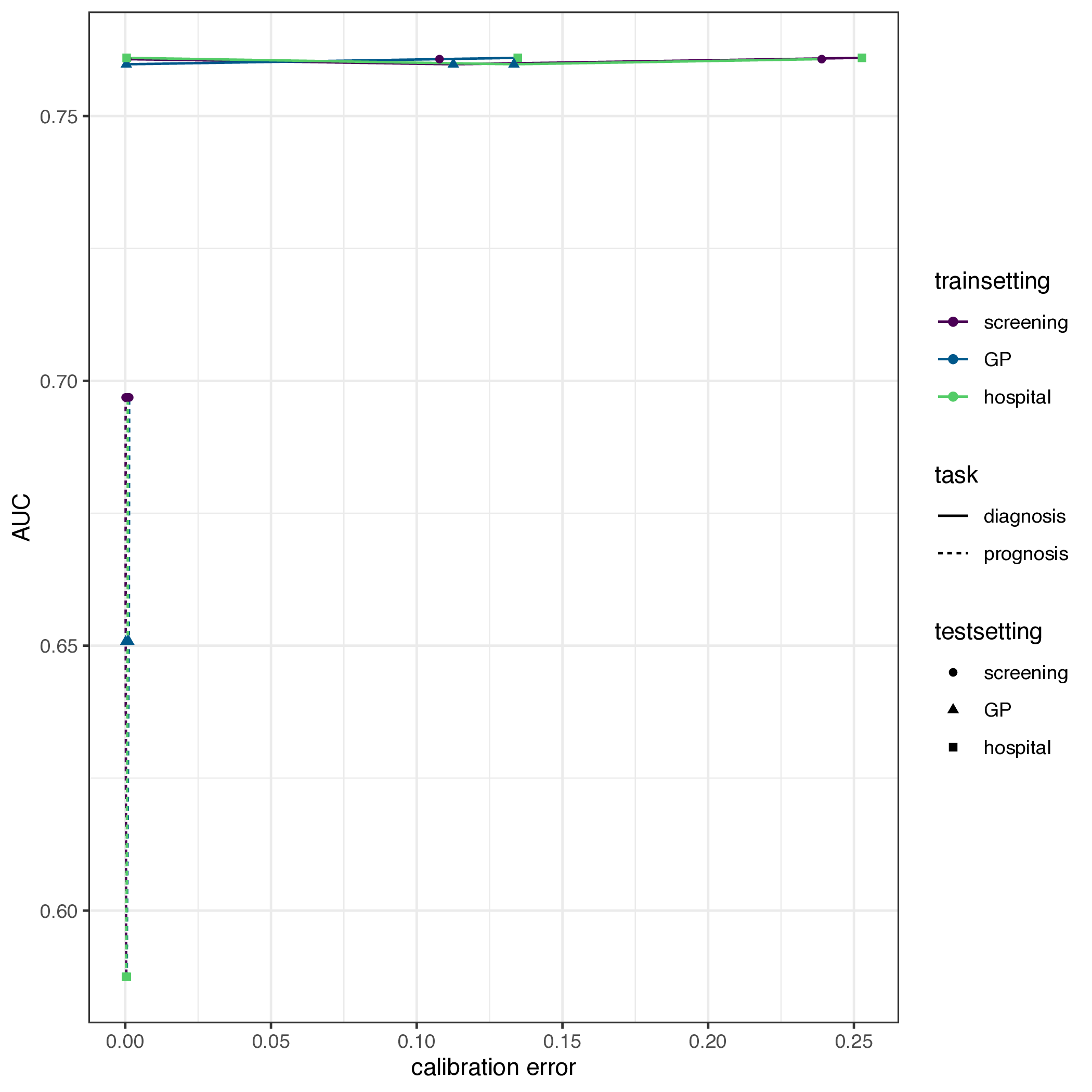
Results

• for each study, extract AUC on internal validation and for each external validation (no calibration data available)
• calculate scaled deviation from internal AUC (\(\delta\))
• theory implies:
  • for prognosis models: \(\delta \neq 0\)
  • for diagnostic models: \(\delta=0\)
• test: variance of \(\delta\) between evaluations of diagnostic or prognostic models (F-test)
• result: \(\text{VAR}(\delta_{\text{diagnostic}})=0.019 \approx 0.122 * \text{VAR}(\delta_{\text{prognostic}})\), p-value\(<0.001\)

Conclusion

• discrimination: a function of features given outcome
• calibration: a function of outcome given outcome
• are we predicting an effect based on its causes (e.g. heart attack, based on cholesterol and age)
• are we predicting a cause based on its effects (infer presence of CVA based on neurological symptoms)
• define shift in case-mix as a change in the marginal distribution of the cause variable
• conclude that in theory:
  • for prognosis models: expect stable calibration, not discrimination
  • for diagnosis models: expect stable discrimination, not calibration
• illustrated with simulation, evaluated on 2030+ prediction model evaluations, one direction of theory seems confirmed
• future work: more empirical validations

Questions:

• how does this align with what you observed?
• where to publish this work?

References

Hond, A. A. H. de. 2023. “From Code to Clinic: Theory and Practice for Artificial Intelligence Prediction Algorithms.” PhD thesis, Leiden University.

Van Calster, Ben, and Andrew J. Vickers. 2015. “Calibration of Risk Prediction Models: Impact on Decision-Analytic Performance.” Medical Decision Making 35 (2): 162–69. https://doi.org/10.1177/0272989X14547233.

Wessler, Benjamin S., Jason Nelson, Jinny G. Park, Hannah McGinnes, Gaurav Gulati, Riley Brazil, Ben Van Calster, et al. 2021. “External Validations of Cardiovascular Clinical Prediction Models: A Large-Scale Review of the Literature.” Circulation: Cardiovascular Quality and Outcomes 14 (8): e007858. https://doi.org/10.1161/CIRCOUTCOMES.121.007858.