Pearl Causal Hierarchy

Causal Inference at Julius reading group

Wouter van Amsterdam

2024-11-06

Table of contents

• The ladder of questions
• The building blocks: structural causal models
• Unpacking an example
• How are these counterfactuals different from the Potential Outcome framework counterfactuals?

Today’s readings:

• Bareinboim’s paper / book chapter: Bareinboim et al. (2022)
• Book of why chapter 1: Pearl and Mackenzie (2018)
• Pearl’s note on hierarchy: Pearl (n.d.)

The ladder of questions

The ladder is a hierarchy of questions

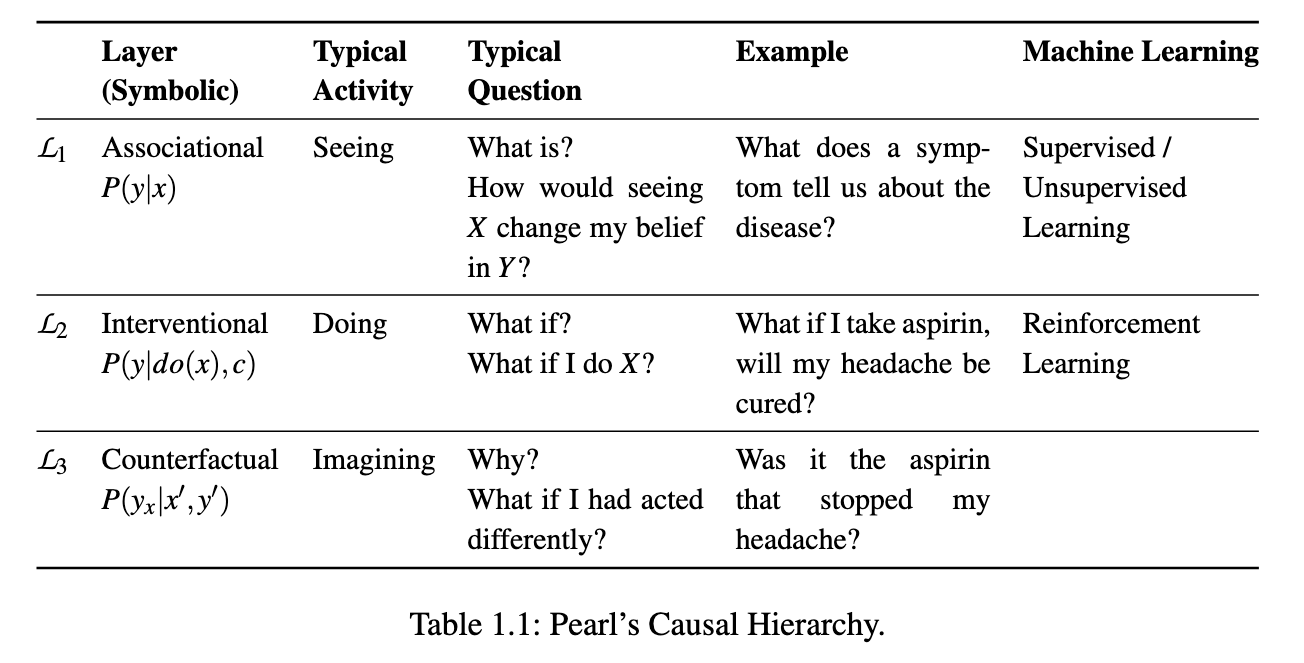
table 1

Notation

• \(X\): treatment (binary, 0,1)
• \(Y\): outcome (binary)
• \(Z\): covariate (age, sex)
• \(p(Y|Z)\): conditional distribution of \(Y\) given \(Z\) (e.g. regression, ‘prediction’)
• \(p(Y_x)\): the causal effect of \(X\) on \(Y\), e.g.:
  • \(p(Y_{X=1}=1)\): the probability that \(Y\) would take value 1 when we would set \(X\) to 1 by intervention
  • \(P(Y_1) - P(Y_0) = \text{ATE}\) (average treatment effect)

Layer 1: association

• What is the relationship between two or more variables?
• required:
  • data (observational / non-experimental): \(p(X,Y,Z)\)
• questions:
  • what is the expected survival for men, and for women? \(p(Y|Z=1)\), \(p(Y|Z=0)\)

Layer 2: intervention

• What happens if we intervene on a variable?
• by how much would survival change if we would treat every patient with a certain drug?
  • this can be made subgroup specific (the conditional average treatment effect: CATE), e.g. covariate \(Z\): \(p(Y_{X=1}|Z) - p(Y_{X=0}|Z)\)
  • when covariate \(Z\) is continuous, every patient has a different CATE, but conceptually this is still the CATE (average over population with same / similar value of \(Z\)), not individual treatment effect
• \(p(Y_{X=1}=1|Z=z)\): the conditional probability that \(Y\) would take value 1 when we would set \(X\) to 1 by intervention, given that \(Z=z\)
  • aka ‘prediction under (hypothertical) intervention’
  • aka ‘potential outcome prediction’
  • aka ‘counterfactual prediction’

Layer 2: intervention, what is required?

1. data where \(X\) is controlled by experimentation (randomized controlled trial)
2. observational data + sufficient assumptions, typically:

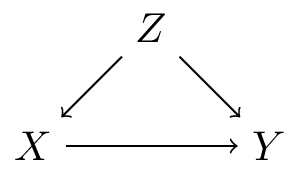
• the directed acyclic graph (DAG) for the variables and no unobserved confounders

DAG 1

Layer 3: counterfactuals

• What would have happened if we had done something else?
• questions:
  • given that the ICU patient got vancomycin and developed acute kidney injury, would she have developed AKI if she had not received vancomycin?
  • \(P(Y_{X=0}=1|Y=1,X=1)\)
• counterfactuals have an element of:
  • something occured in the world (a fact)
  • what if we went back to the world and changed a thing, what would have occured then? (a counterfact)
• required:
  • knowledge of functional relationships

The hierarchy, what are the worlds?

Layer 2: directed acyclic graph (DAG)

1. association: the world as it is
2. intervention: the world as we could be under an intervention (as it would be / is in an experiment)
3. counterfactuals: the world as it was, and how it might have been if something had been different

The hierarchy, what are the worlds?

1. one real world
2. one hypothetical world (or real in experiment)
3. one real world and a hypothetical world

What are the layers useful for?

1. association: description, prediction (know what to expect when observing the world with hands on our backs)
2. intervention: policy making, decision making (know what to expect when we change the world)
3. counterfactuals: explanation, understanding:

• drug side effects
• digital twins: a digital representation of a physical object or system: typically assumes counterfactual level knowledge, e.g. Sel et al. (2024)
• questions of fairness

The building blocks: structural causal models

What is a SCM?

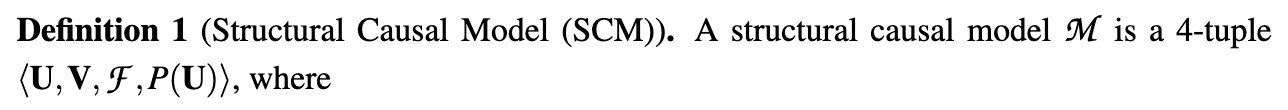
definition of SCM

• \(U\) is a set of background variables, also called exogenous variables, that are determined by factors outside the model;
• \(V\) is a set \(\{V_1,V_2,...,V_n\}\) of variables, called endogenous, that are determined by other variables in the model - that is, variables in \(U\cup V\);
• \(F\) is a set of functions \(\{ f_1, f_2,..., f_n\}\) such that each fiis a mapping from (the respective domains of) \(U_i \cup Pa_i \to V_i\), where \(U_i \subset U\), \(Pa_i \subset V - Vi\), and the entire set \(F\) forms a mapping from \(U\) to \(V\). That is, for \(i = 1,...,n\), each \(f_i \in F\) is such that

\[v_i \leftarrow f_i(pa_i, u_i)\]

• i.e., it assigns a value to \(V_i\) that depends on (the values of) a select set of variables in \(U \cup V\); and
• \(P(U)\) is a probability function defined over the domain of \(U\).

How are SCMs and DAGs related?

A recursive SCM implies a DAG, by following the order of arguments in the set of functions \(F\). E.G.:

\[ F = \begin{cases} Z \leftarrow f(U_Z) \end{cases} \]

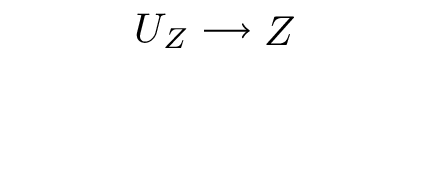
How are SCMs and DAGs related?

A recursive SCM implies a DAG, by following the order of arguments in the set of functions \(F\). E.G.:

\[ F = \begin{cases} Z \leftarrow f(U_Z) \\ X \leftarrow f(Z, U_X) \end{cases} \]

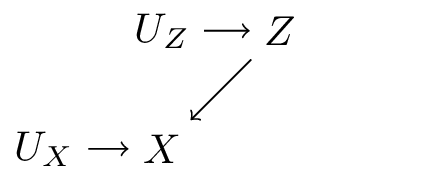
How are SCMs and DAGs related?

A recursive SCM implies a DAG, by following the order of arguments in the set of functions \(F\). E.G.:

\[ F = \begin{cases} Z \leftarrow f(U_Z) \\ X \leftarrow f(Z, U_X) \\ Y \leftarrow f(X, Z, U_Y) \end{cases} \]

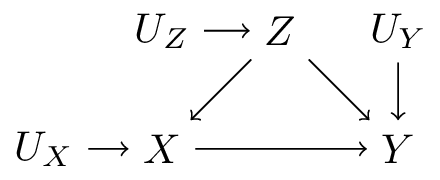
How are SCMs and DAGs related?

• A (recursive) SCM implies a DAG,
• but has strictly more information as not only the functional arguments are known,
• but also the functions themselves

Intervening in a SCM: a submodel

A recursive SCM implies a DAG, by following the order of arguments in the set of functions \(F\). E.G.:

\[ F = \begin{cases} Z \leftarrow f(U_Z) \\ X \leftarrow X' \\ Y \leftarrow f(X, Z, U_Y) \end{cases} \]

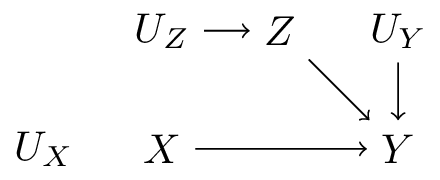
We can compute the effect of an action by replacing one \(f\) with a constant, e.g. \(X \leftarrow X'\), keep everything else the same, and evaluate the outcomes

Intermezzo: critique on the hierarchy

• The Pearl Causal Hierarchy is a hiearchy of questions
• Some (rightly) argue that the ‘higher’ we go, the more prior assumptions are needed, and the less we rely on experiments
• In a sense of empirical science, the hierarchy is upside down

Theorem 1

Theorem 1

Unpacking an example

example 7a

\(X\): treatment, \(Y\): outcome, \(U_1, U_2\): exogenous noise variables; \(p(U_1=1)=p(U_2=1)=0.5\)

\[ F = \begin{cases} X \leftarrow U_1 \\ Y \leftarrow U_2 \end{cases} \]

• treatment: coin flip
• survival: coin flip (not affected by \(X\))

\[ F' = \begin{cases} X \leftarrow 1_{U_1=U_2} \\ Y \leftarrow U_1 + 1_{X=1,U+1=0,U_2=1} \end{cases} \]

• survival: affected by \(X\)

example 7a

\[ F = \begin{cases} X \leftarrow U_1 \\ Y \leftarrow U_2 \end{cases} \]

\[ F' = \begin{cases} X \leftarrow 1_{U_1=U_2} \\ Y \leftarrow U_1 + 1_{X=1,U+1=0,U_2=1} \end{cases} \]

• both models: same level 1 (observational) distribution \(p(X,Y)\)
• different level 2: \(Y_{X}\)
• cannot tell models apart from observatoinal data alone (i.e. causal effect not identified)

example 7b

\(X\): treatment, \(Y\): outcome, \(U_1, U_2\): exogenous noise variables; \(p(U_1=1)=p(U_2=1)=0.5\)

\[ F = \begin{cases} X \leftarrow U_1 \\ Y \leftarrow U_2 \end{cases} \]

\[ F' = \begin{cases} X \leftarrow U_1 \\ Y \leftarrow X U_2 + (1-X)(1-U_2) \end{cases} \]

• ‘the effect of treatment is determined by the coinflip’

• both models: same level 2 (interventional) distributions
• different level 3: \(Y_{X=0}=1|X=1,Y=0)\)
• cannot tell models apart from level 2 data alone

How are these counterfactuals different from the Potential Outcome framework counterfactuals?

Potential outcomes framwork:

Image two possible futures for a patient

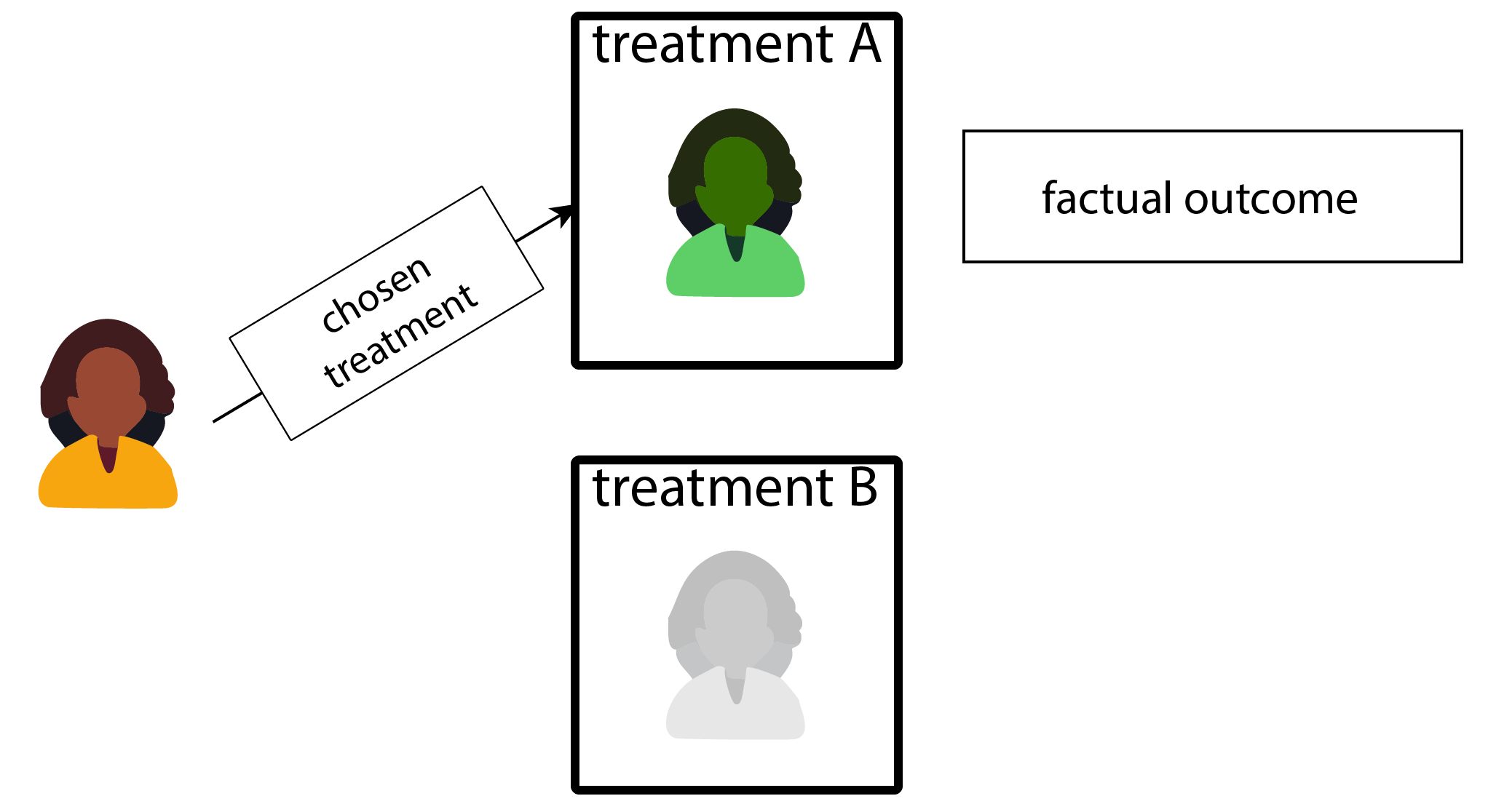
Potential outcomes vs SCMs

• why I like the term potential outcomes: it has a clear sense of futures
• counterfactual in the PO framework: has a clear definition and interpretation
• what I don’t like: using the term counterfactual outcomes when the potential outcomes are meant, and neither has occured yet
  • e.g. counterfactual prediction
• in the SCM frawmwork, counterfactuals are closer to the word:
  • a fact has been observed (the real world)
  • a counter fact has been asked
  • this actually conditions on the observed factual data (often not the case in PO framework)
    • “given that the ICU patient got vancomycin and developed acute kidney injury, would she have developed AKI if she had not received vancomycin?”

References

Bareinboim, Elias, Juan Correa, Duligur Ibeling, and Thomas Icard. 2022. “On Pearl’s Hierarchy and the Foundations of Causal Inference (1st Edition).” In Probabilistic and Causal Inference: The Works of Judea Pearl, edited by Hector Geffner, Rita Dechter, and Joseph Halpern, 507–56. ACM Books.

Pearl, Judea. n.d. “The Three Layer Causal Hierarchy.” Accessed November 4, 2024.

Pearl, Judea, and Dana Mackenzie. 2018. The Book of Why: The New Science of Cause and Effect. 1st edition. New York: Basic Books.

Sel, Kaan, Deen Osman, Fatemeh Zare, Sina Masoumi Shahrbabak, Laura Brattain, Jin-Oh Hahn, Omer T. Inan, et al. 2024. “Building Digital Twins for Cardiovascular Health: From Principles to Clinical Impact.” Journal of the American Heart Association 13 (19): e031981. https://doi.org/10.1161/JAHA.123.031981.