Causality and prediction: developing and validating models for decision making
Causal Data Science Special Interest Group - Utrecht
Department of Data Science Methods, Julius Center, University Medical Center Utrecht
2024-05-16
Prediction versus causal inference
Prediction
- have some features X (patient characteristics, medical images, lab results)
- define relevant outcome Y (e.g. 1-year survival, blood pressure, treatment complication)
- build prediction model f:X→Y that predicts Y from X, e.g.:
θ∗=argmin
Hoping that
\lim_{n \to \infty} f_{\theta^*} = E[Y|X]
Prediction: typical approach
- define population, start a (prospective) longitudinal cohort
- measure X at prediction baseline
- follow-up patients to measure Y
- fit model f to \{x_i,y_i\}
- evaluate prediction performance with e.g. discrimination, calibration, R^2
Causal inference
y^0:= imaginative outcome if I don’t treat the patient
\begin{align} y^0 &= \mu_0 + \epsilon, \quad \epsilon \overset{\mathrm{iid}}{\sim} N(0,\sigma)\\ \end{align}
this formula together with distribution over error term gives rise to a distribution over the outcome when intervening on treatment (i.e. an interventional distribution)
P(Y=y|\text{do}(T=0))
Causal inference
y^0:= imaginative outcome if I don’t treat the patient
y^1:= imaginative outcome if I do treat
\begin{align} y^0 &= \mu_0 + \epsilon, \quad \epsilon \overset{\mathrm{iid}}{\sim} N(0,\sigma) \to &P(Y=y|\text{do}(T=0))\\ y^1 &= \mu_1 + \epsilon, \quad \epsilon \overset{\mathrm{iid}}{\sim} N(0,\sigma) \to &P(Y=y|\text{do}(T=1)) \end{align}
\begin{align} \text{treatment effect} &:= E[y^1] - E[y^0] = \mu_1 - \mu_0 \\ &:= E[Y|\text{do}(T=1)] - E[Y|\text{do}(T=0)] \end{align}
Causal inference: typical approach
- define target population and targeted treatment comparison
- run randomized controlled trial, randomizing treatment allocation
- measure patient outcomes
- estimate parameter that summarizes average treatment effect (ATE)
What if you cannot do a (big enough) RCT?
Emulate / approximate the ideal trial in observational data you do have, using causal inference techniques
(which rely on untestable assumptions)
Causal inference versus prediction
prediction
- typical estimand E[Y|X]
- typical study: longitudinal cohort
- typical interpretation: X predicts Y
- primary use: know what Y to expect when observing X assuming no change in joint distribution
causal inference
- typical estimand E[Y|\text{do}(T=1)] - E[Y|\text{do}(T=0)]
- typical study: RCT
- typical interpretation: causal effect of T on Y
- primary use: know what treatment to give
The in-between: using prediction models for (medical) decision making
Using prediction models for decision making is often thought of as a good idea
For example:
- give chemotherapy to cancer patients with high predicted risk of recurrence
- give statins to patients with a high risk of a heart attack
TRIPOD+AI on prediction models (collinsTRIPODAIStatement2024?)
“Their primary use is to support clinical decision making, such as … initiate treatment or lifestyle changes.”
This may lead to bad situations when:
- ignoring the treatments patients may have had during training / validation
- only considering measures of predictive accuracy as sufficient evidence for safe deployment
- predictive accuracy (AUC) may be measured pre- or post-deployment of the model
When accurate prediction models yield harmful self-fulfilling prophecies
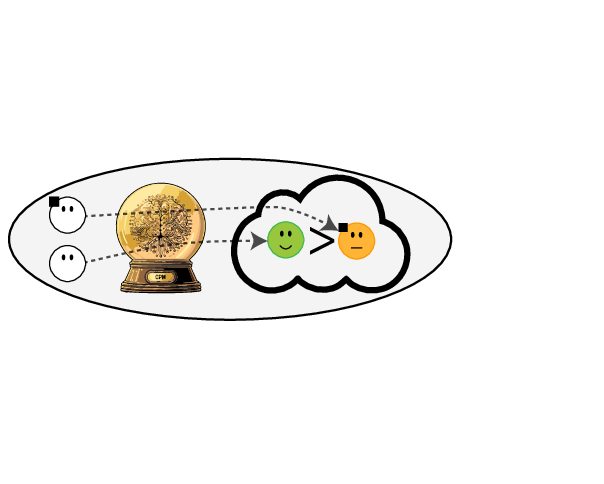
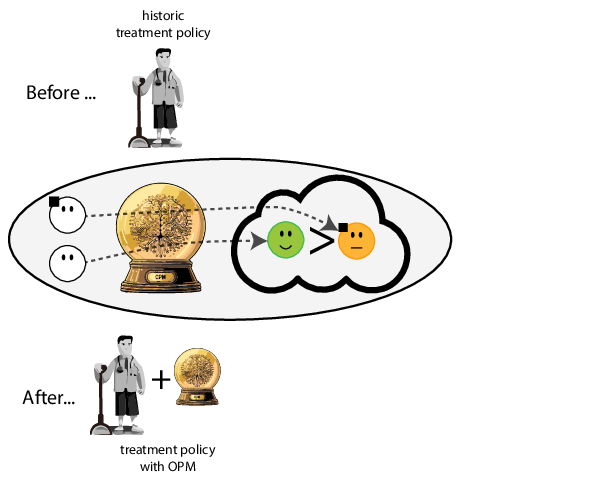
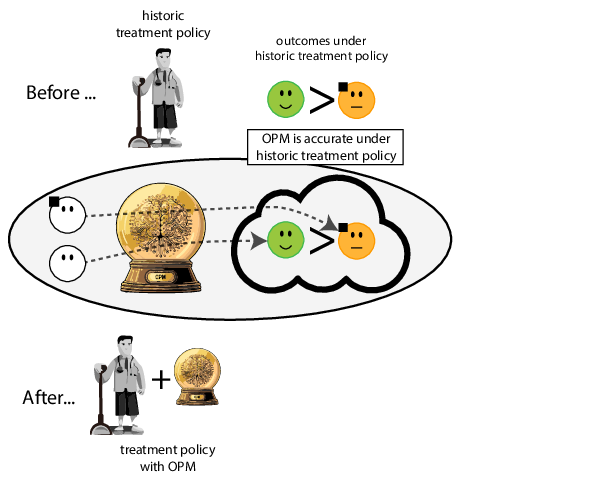
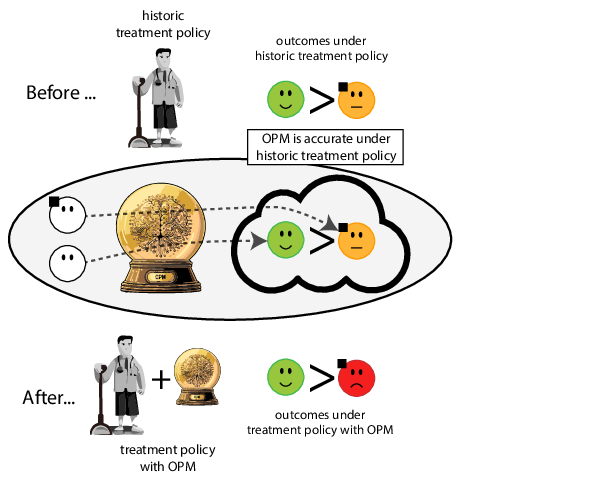
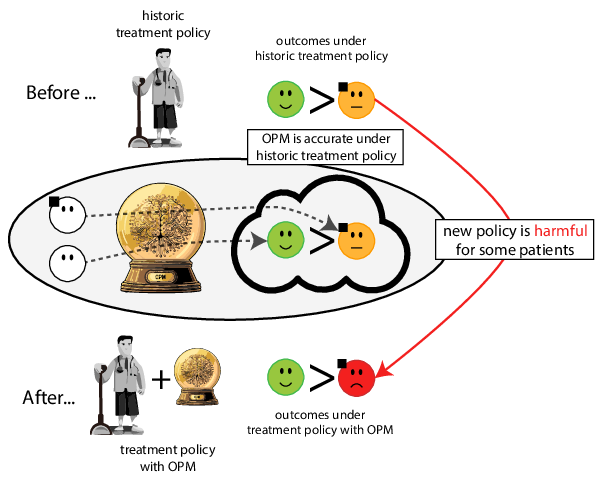
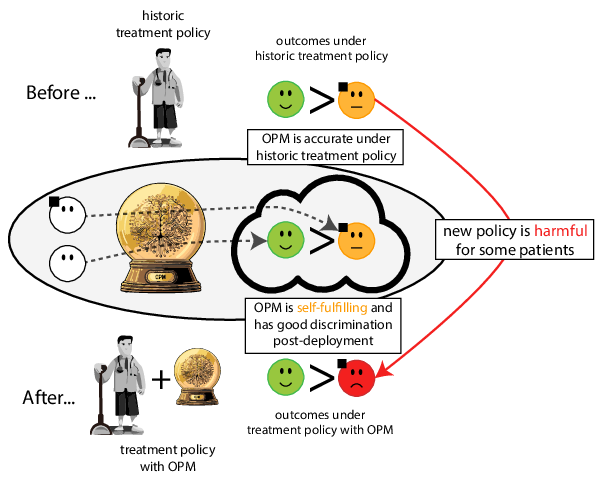
Prediction modeling is very popular in medical research
Tip
building models for decision support without regards for the historic treatment policy is a bad idea
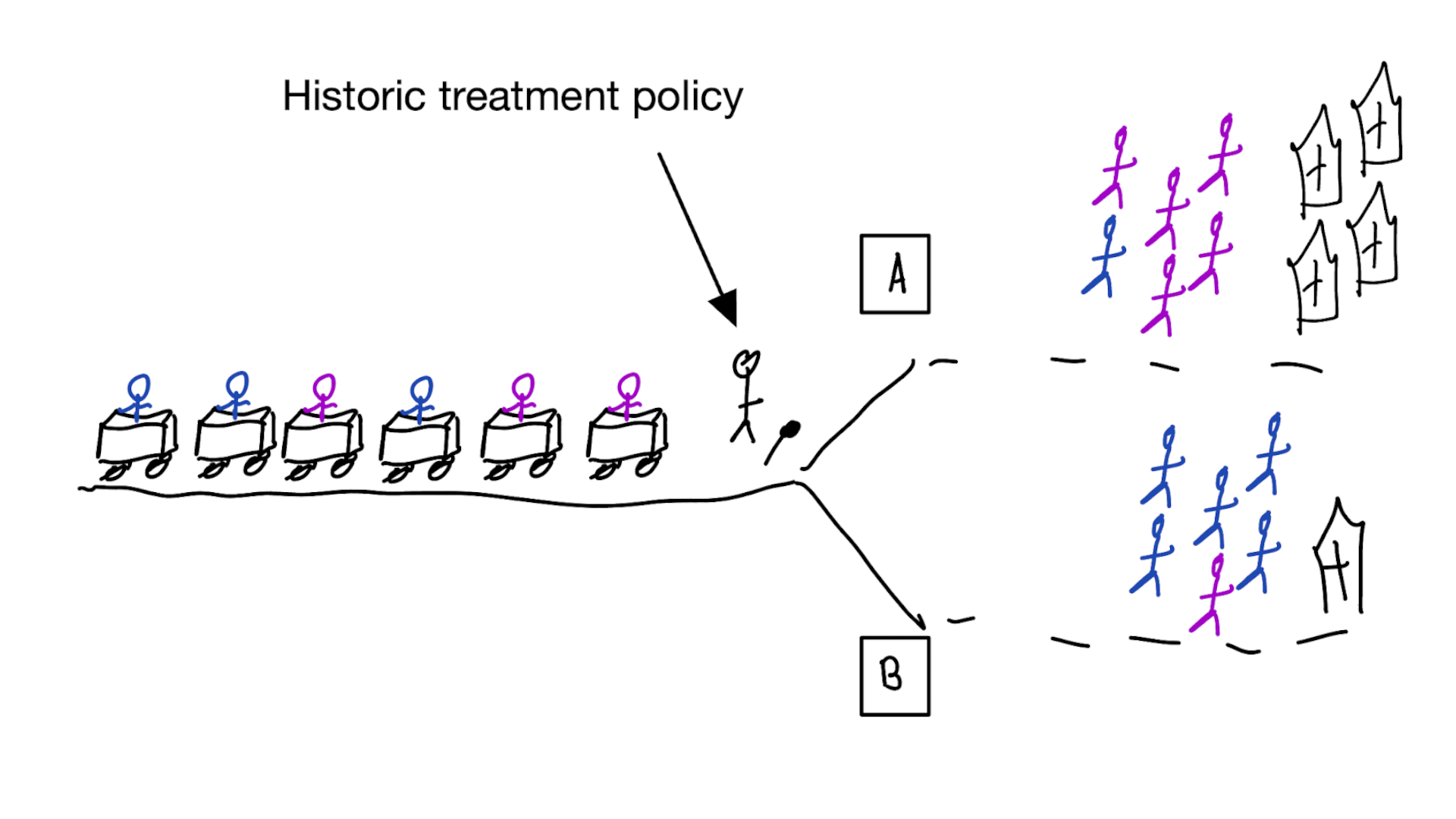
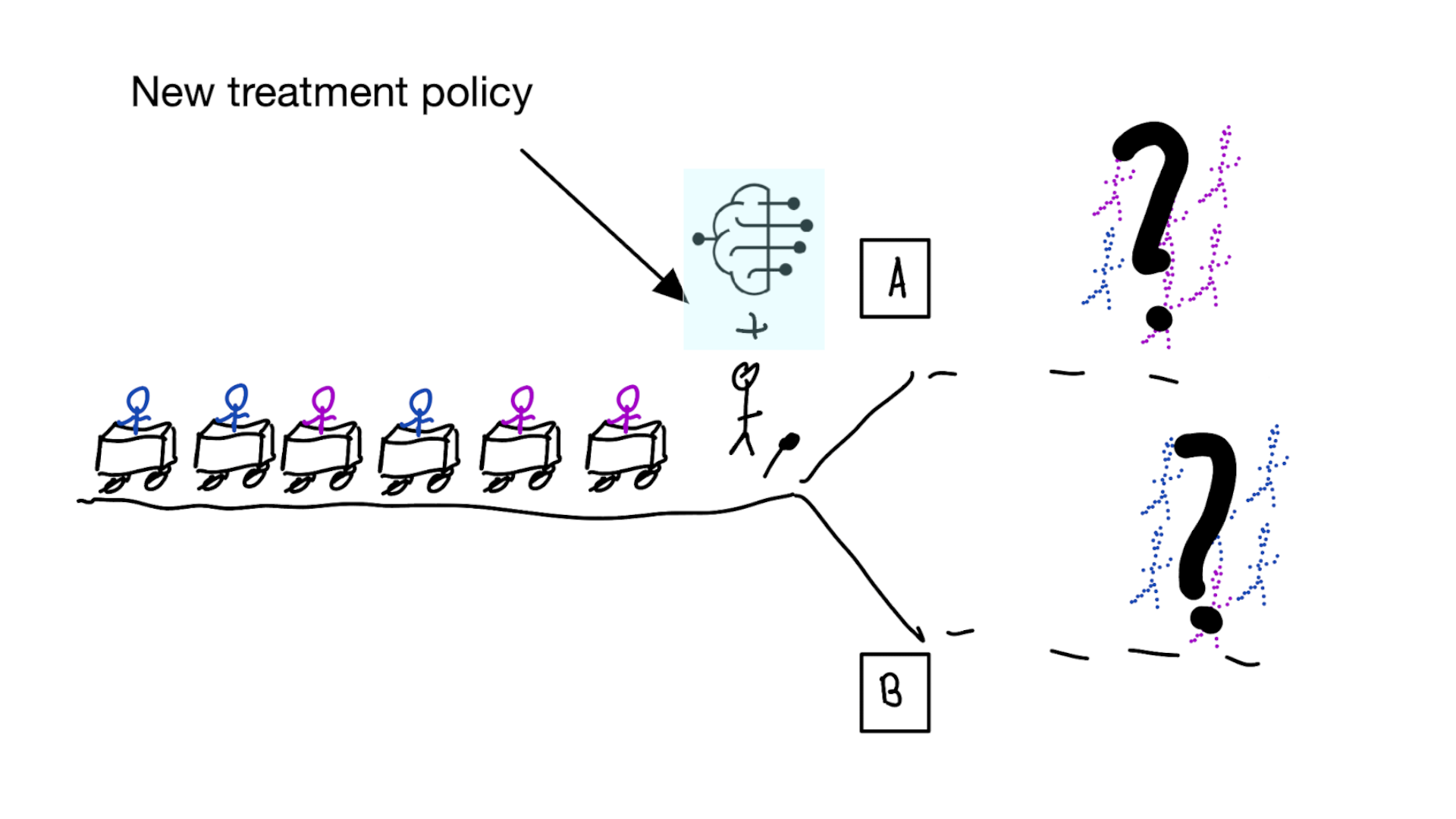
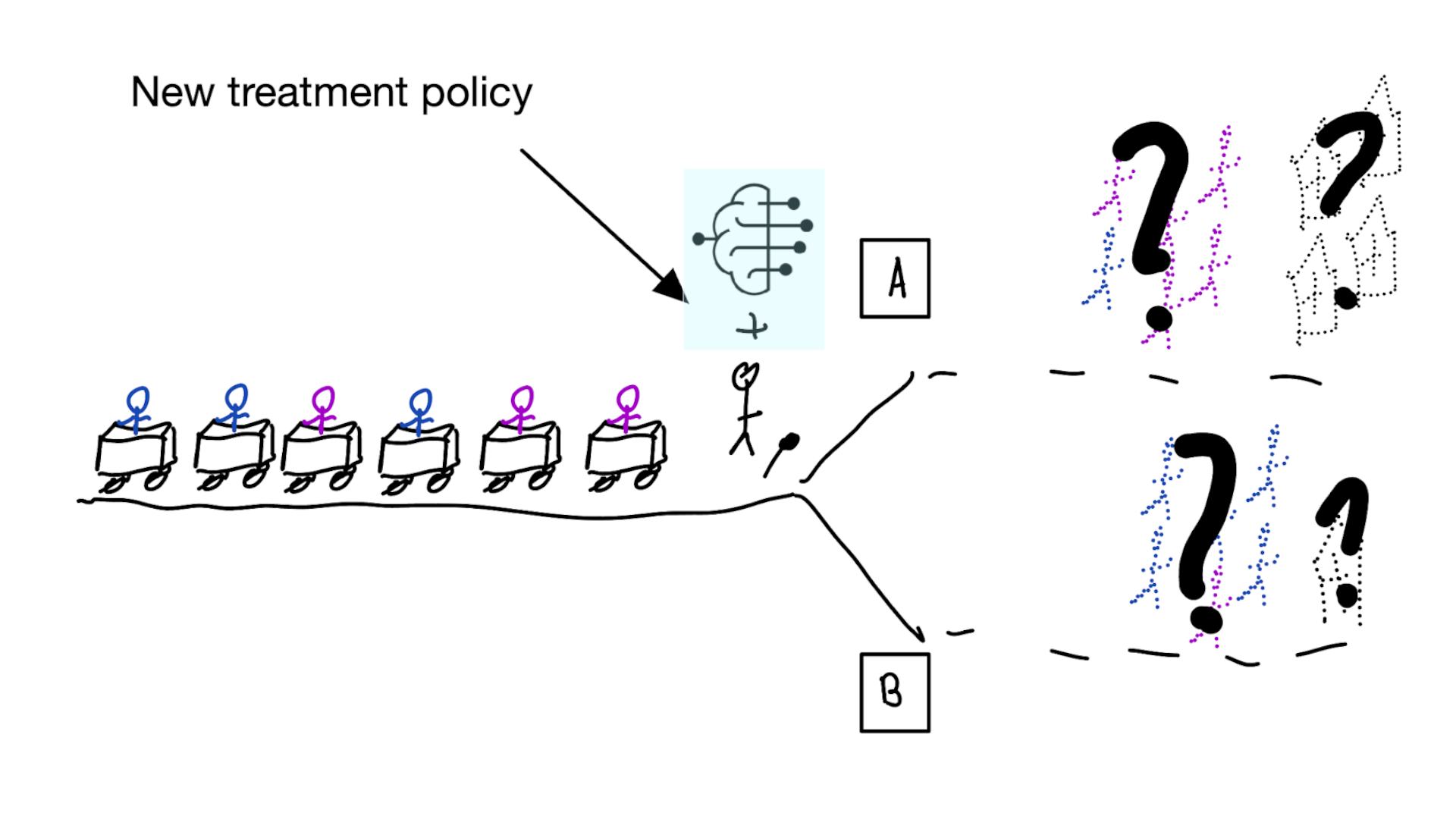
Note
The question is not “is my model accurate before / after deploytment”, but did deploying the model improve patient outcomes?
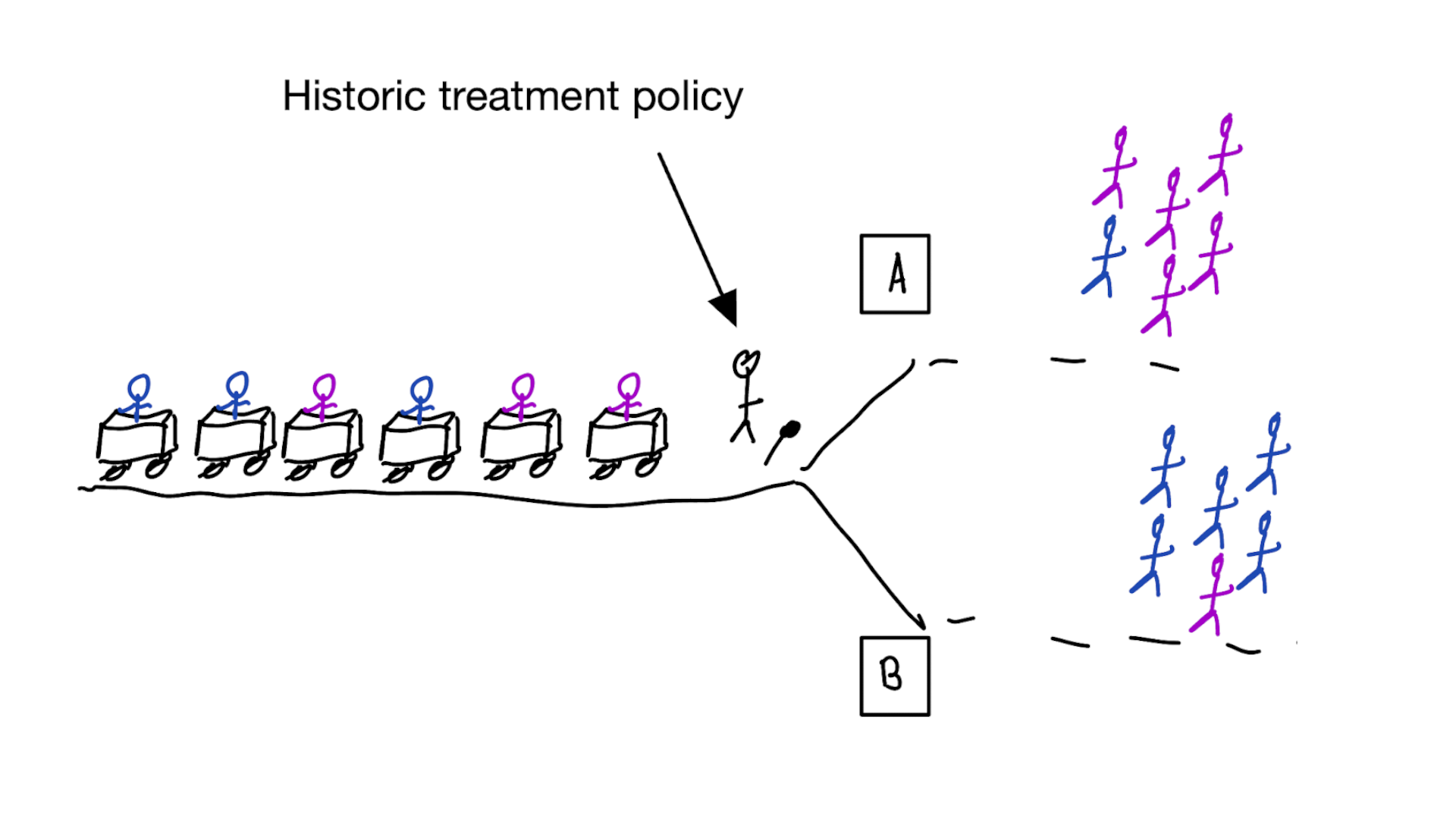
Treatment-naive risk models
\begin{align} E[Y|X] \class{fragment}{= E[E_{t~\sim \pi_0(X)}[Y|X,t]]} \end{align}
Is this obvious?
Tip
It may seem obvious that you should not ignore historical treatments in your prediction models, if you want to improve treatment decisions, but many of these models are published daily, and some guidelines even allow for implementing these models based on predictve performance only
Recommended validation practices do not protect against harm
because they do not evaluate the policy change
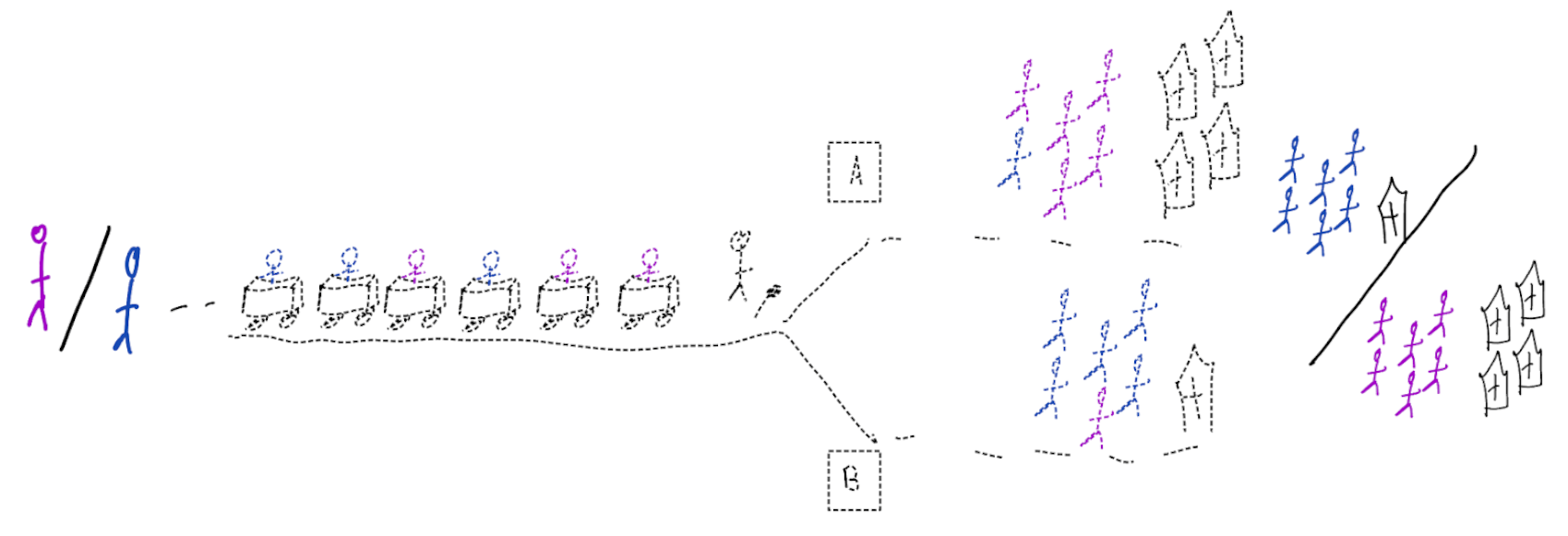
Bigger data does not protect against harmful risk models
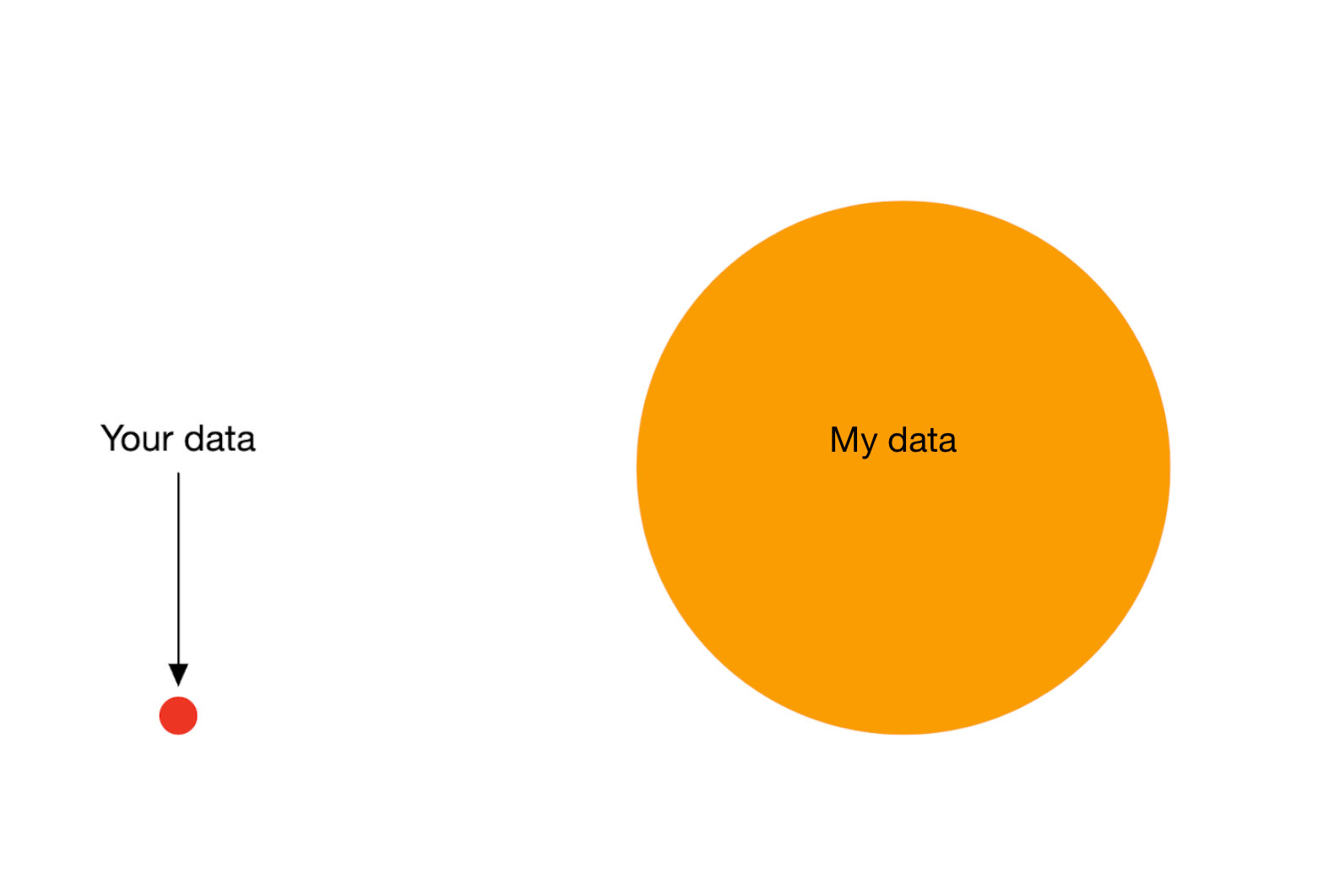
More flexible models do not protect against harmful risk models
Gap between prediction accuracy and value for decision making
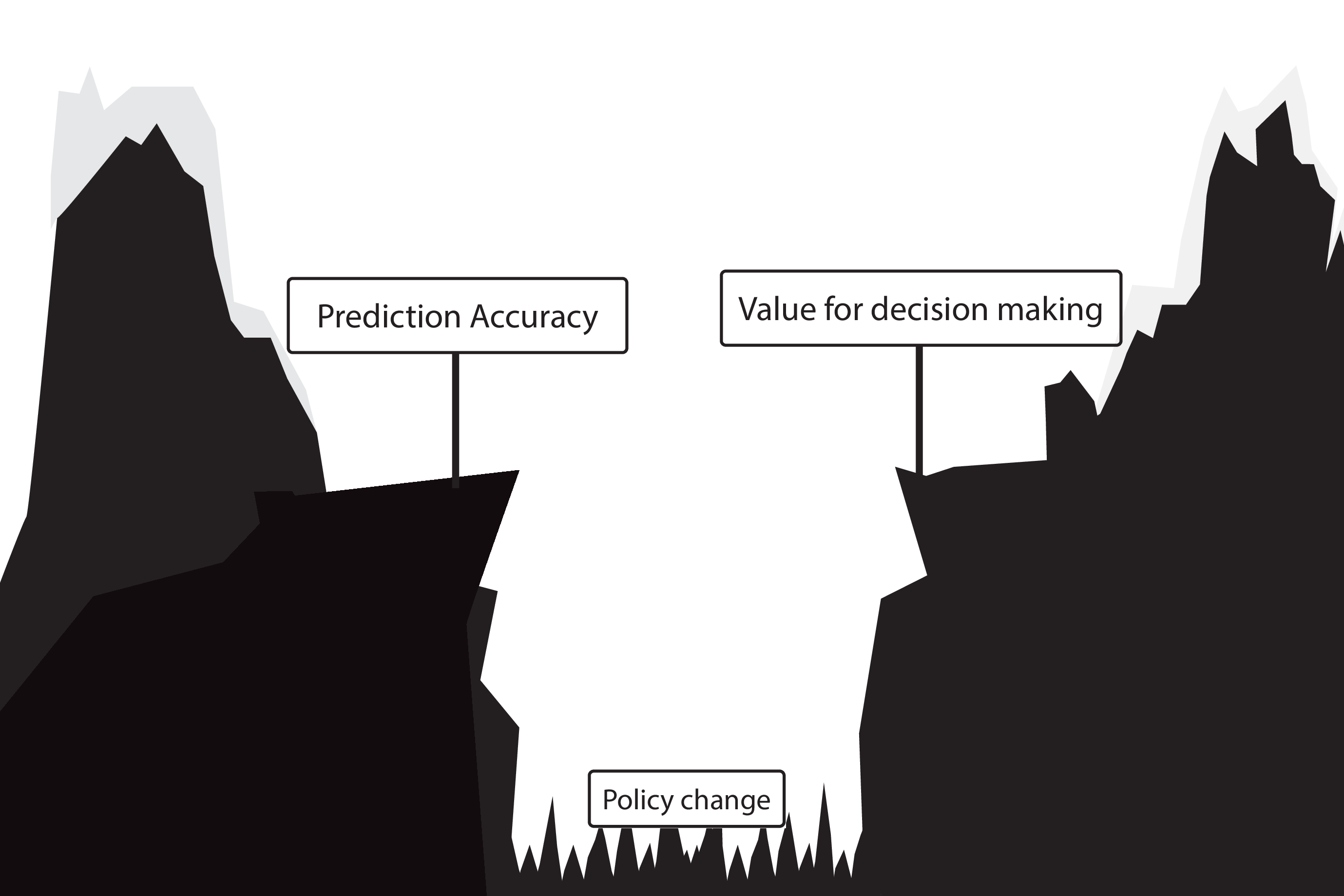
What to do?
What to do?
- Evaluate policy change (cluster randomized controlled trial)
- Build models that are likely to have value for decision making
Building and validating models for decision support
Deploying a model is an intervention that changes the way treatment decisions are made
How do we learn about the effect of an intervention?
With causal inference!
- for using a decision support model, the unit of intervention is usually the doctor
- randomly assign doctors to have access to the model or not
- measure differences in treatment decisions and patient outcomes
- this called a cluster RCT
- if using model improves outcomes, use that one
Using cluster RCTs to evaluated models for decision making is not a new idea (Cooper et al. 1997)
“As one possibility, suppose that a trial is performed in which clinicians are randomized either to have or not to have access to such a decision aid in making decisions about where to treat patients who present with pneumonia.”
What we don’t learn
was the model predicting anything sensible?
So build prediction models and trial them?
Not a good idea
- baking a cake without a recipe
- hoping it turns into something nice
- not pleasant to people that need to taste the experiment
- (i.e. patients may have side-effects / die)
Models that are likely to be valuable for decision making
- prediction under hypothetical interventions (prediction-under-intervention) models predict expected outcomes under the hypothetical intervention of giving a certain treatment
Hilden and Habbema on prognosis (Hilden and Habbema 1987)
“Prognosis cannot be divorced from contemplated medical action, nor from action to be taken by the patient in response to prognostication.”
- whereas treatment-naive prediction models average out over the historic treatment policy, prediction-under-intervention allows the user to select a treatment option
- prediction-under-intervention is not a new idea, but language and methods on causality have come a long way since (Hilden and Habbema 1987).
Estimand for prediction-under-intervention models
What is the estimand?
- prediction: E[Y|X]
- treatment effect: E[Y|\text{do}(T=1)] - E[Y|\text{do}(T=0)]
- prediction-under-intervention: E[Y|\text{do}(T=t),X]
using treatment naive prediction models for decision support
prediction-under-intervention
Estimating prediction-under-intervention models
- the estimand E[Y|\text{do}(T=t),X] is an interventional distribution
- RCTs randomly sample from interventional distributions
- prediction-under-intervention models may be estimated and evaluated in RCT data
- however, RCTs are typically designed to estimate a single parameter
- prediction models need more data
- in comes causal inference from observational data?
Challenges with observational data
- assumption of no unobserved confounding may be hard to justify
- but there’s more between heaven (RCT) and earth (confounder adjustment)
- proxy-variable methods
- constant relative treatment effect assumption
- diff-in-diff
- instrumental variable analysis (high variance estimates)
- front-door analysis
Proxy variables?
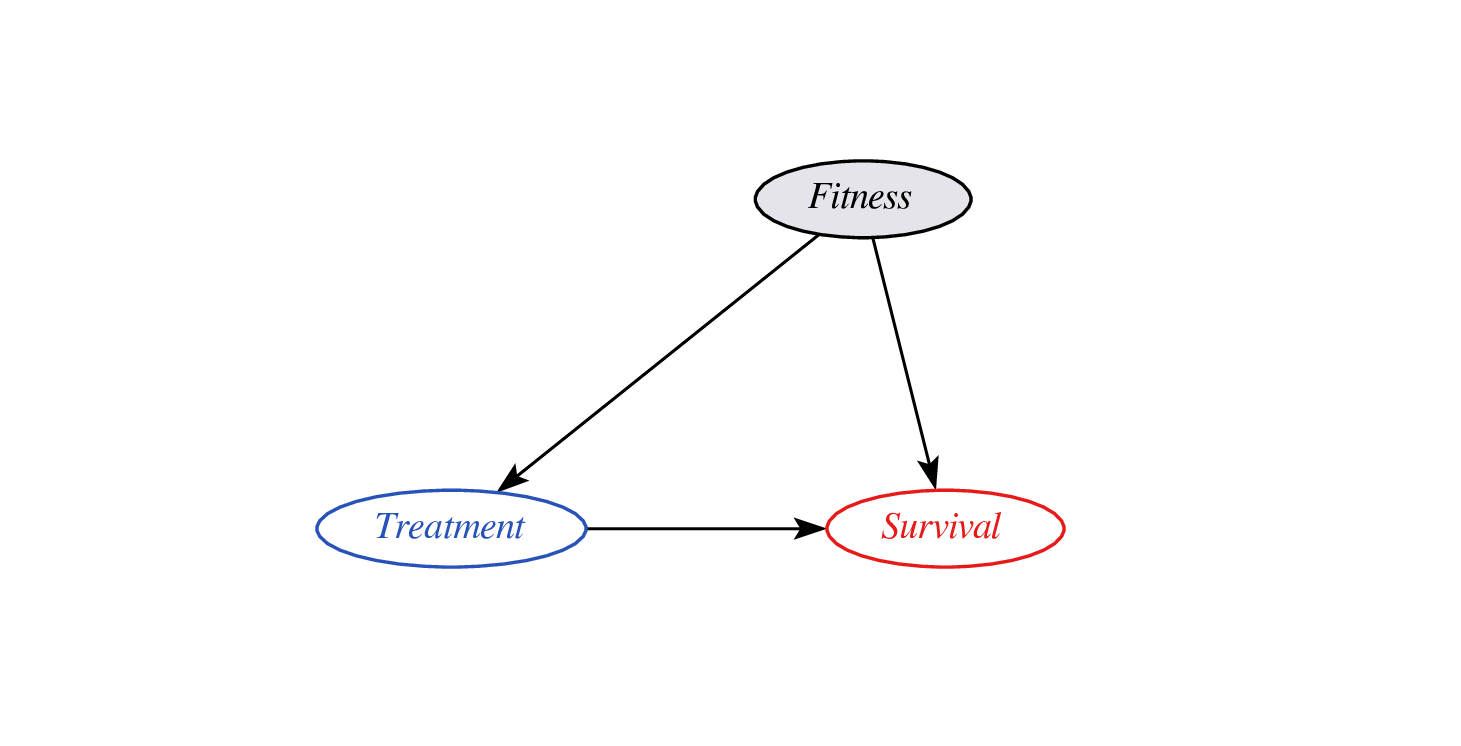
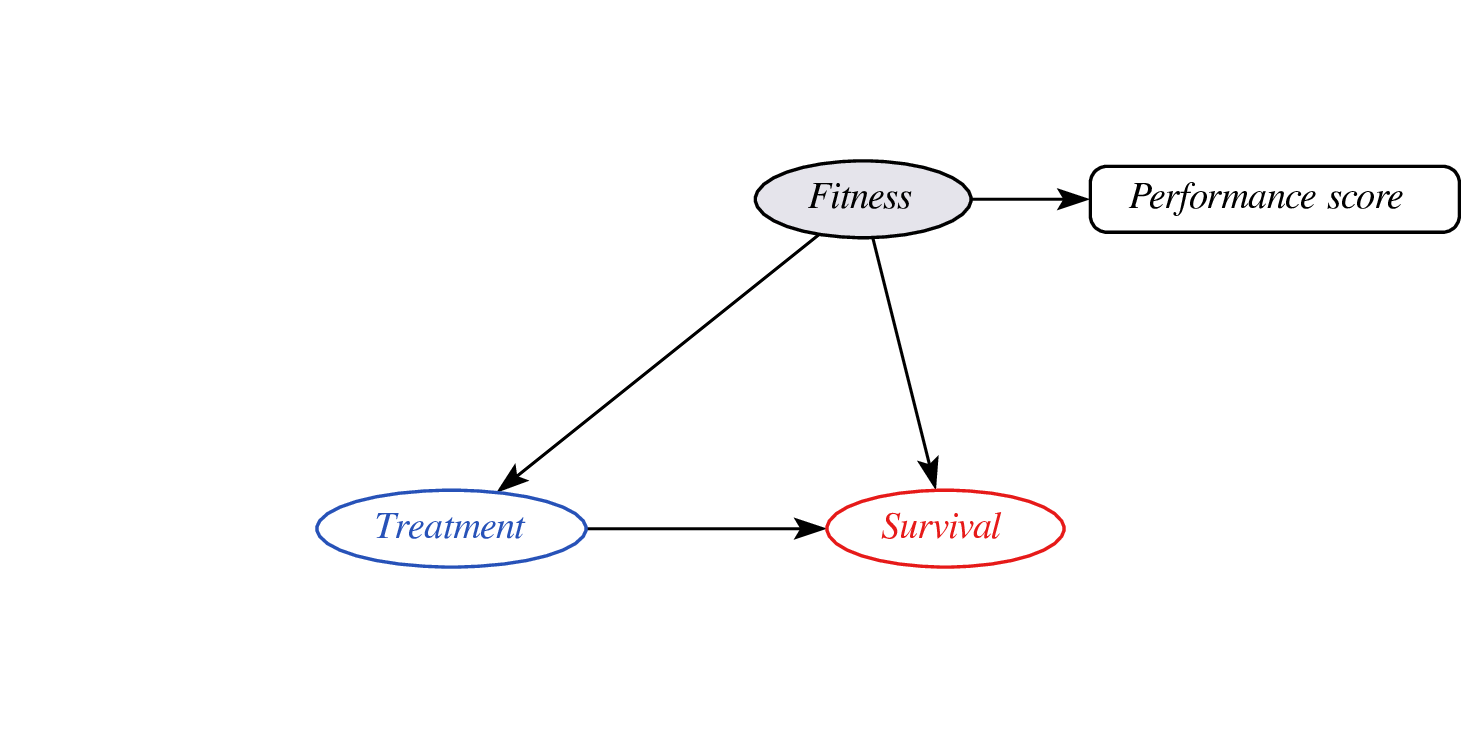
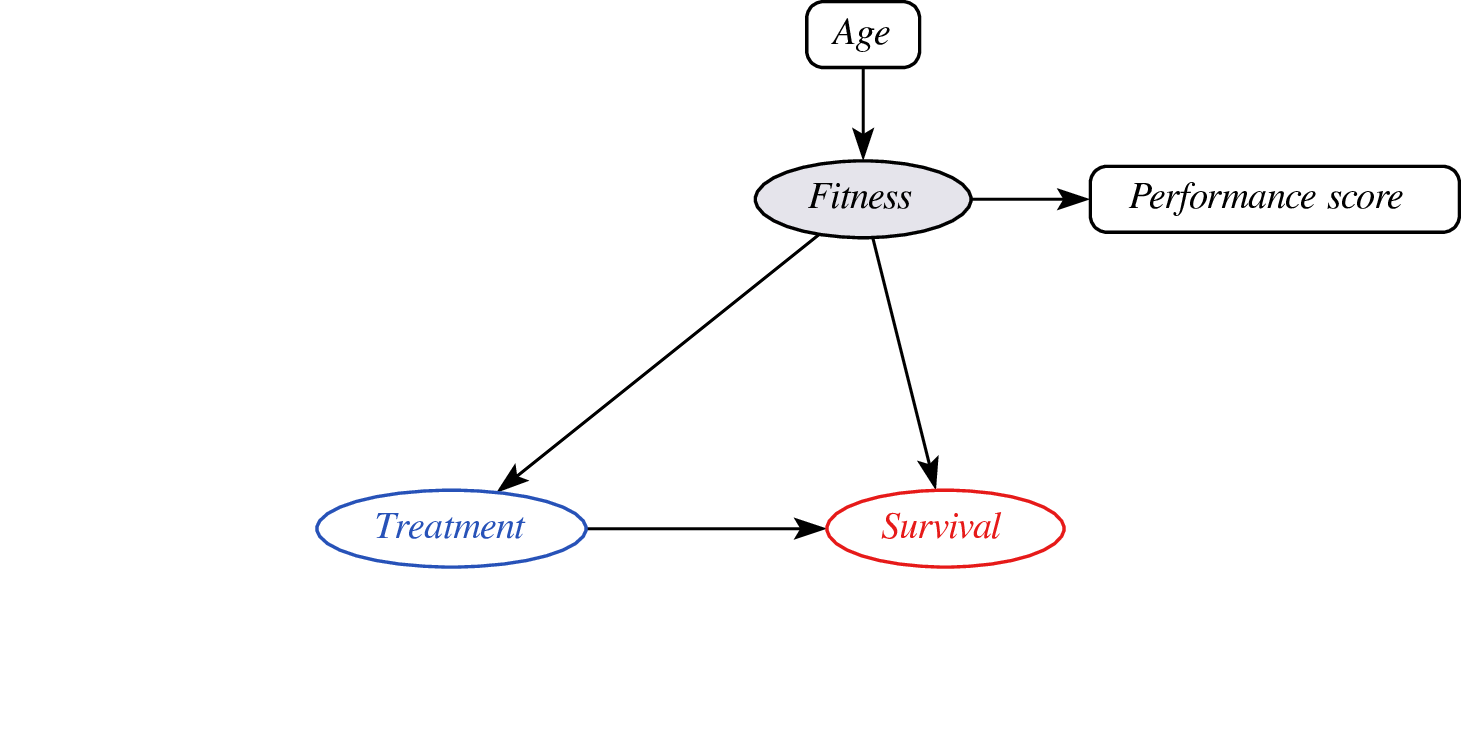
- problem: didn’t observe confounder fitness so cannot do confounder adjustment
- instead, leverage assumptions on confounder - proxy relationship (e.g. monotonicity)
- effect may still be identifyable (van Amsterdam et al. 2022)
Constant relative treatment effect?
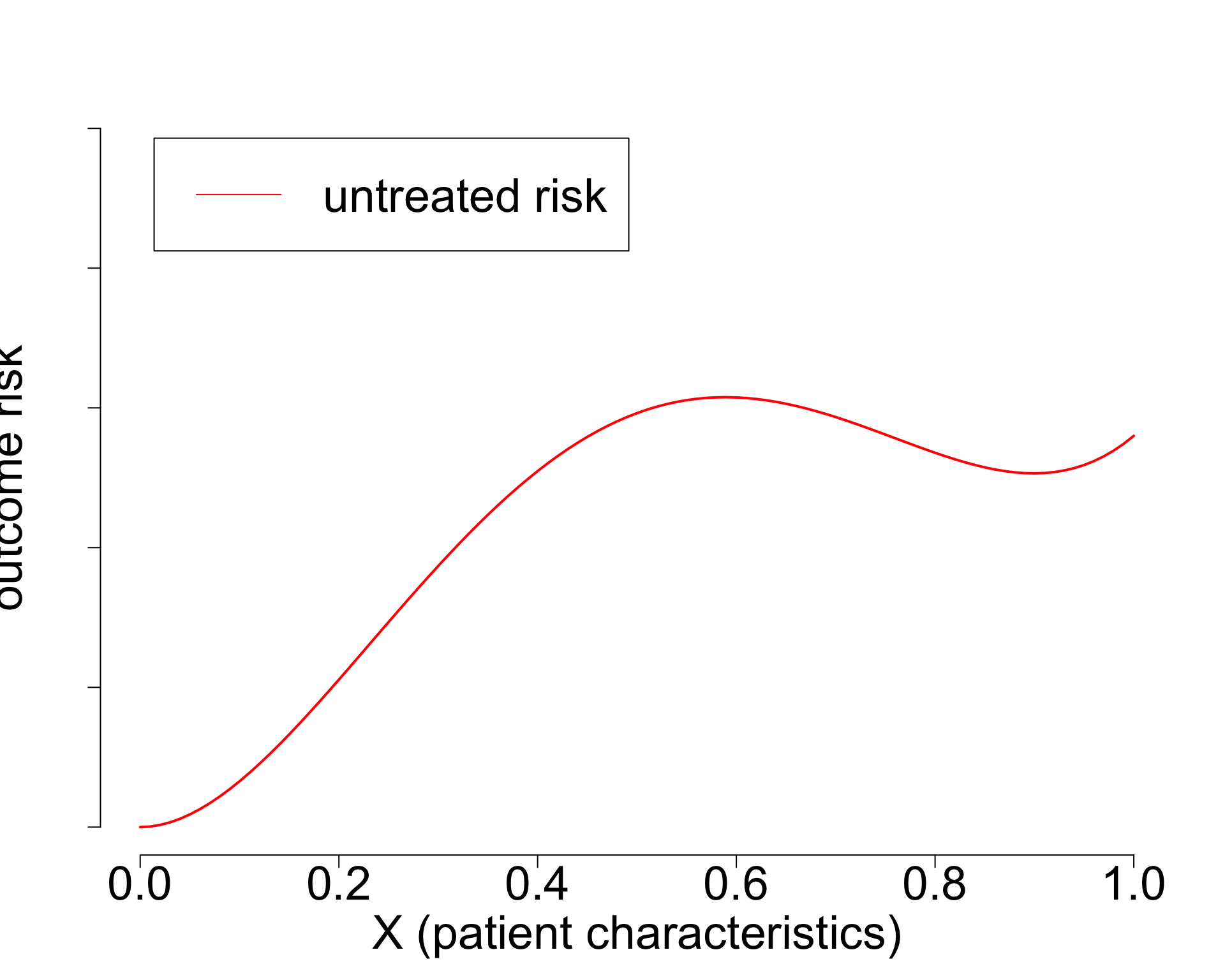
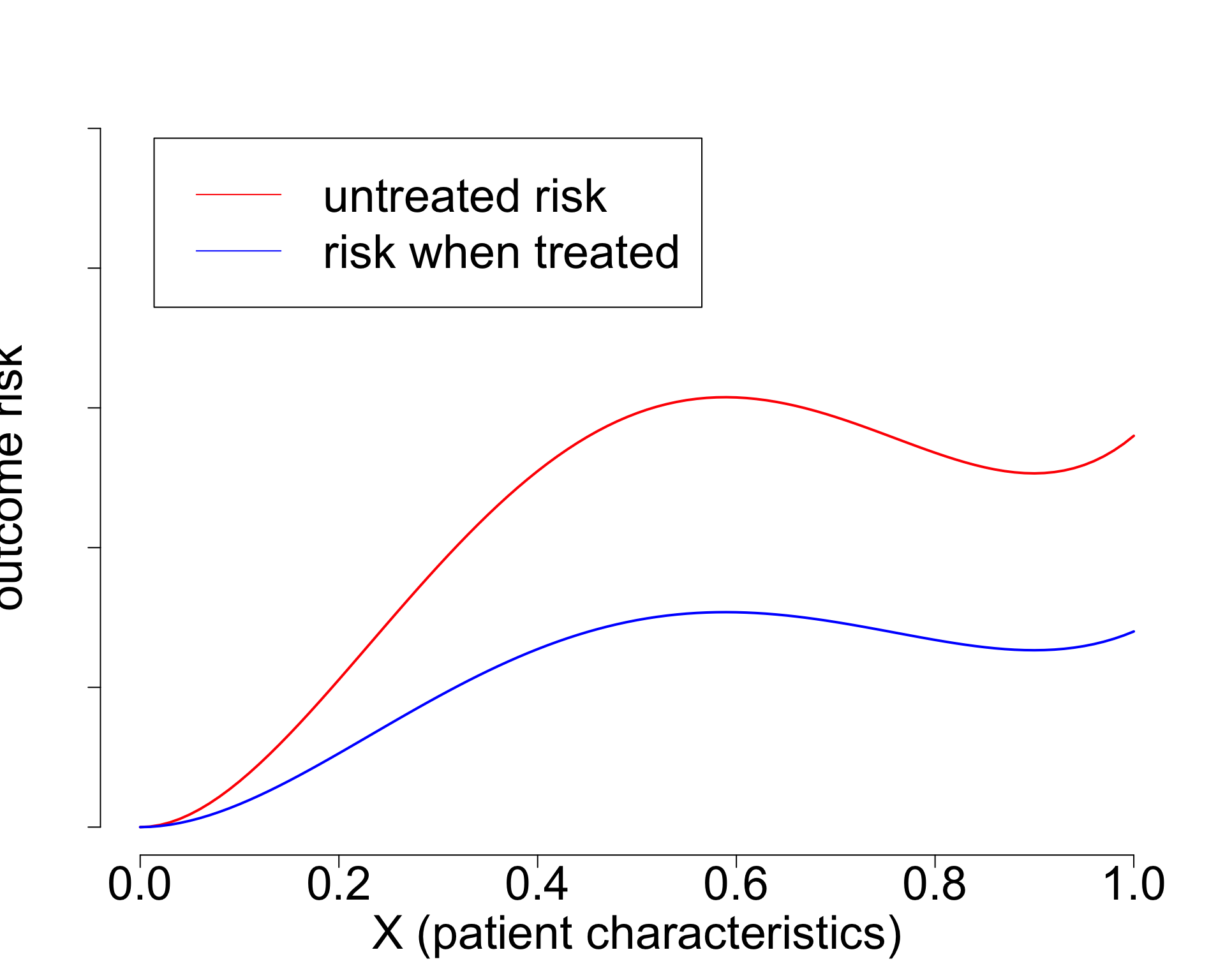
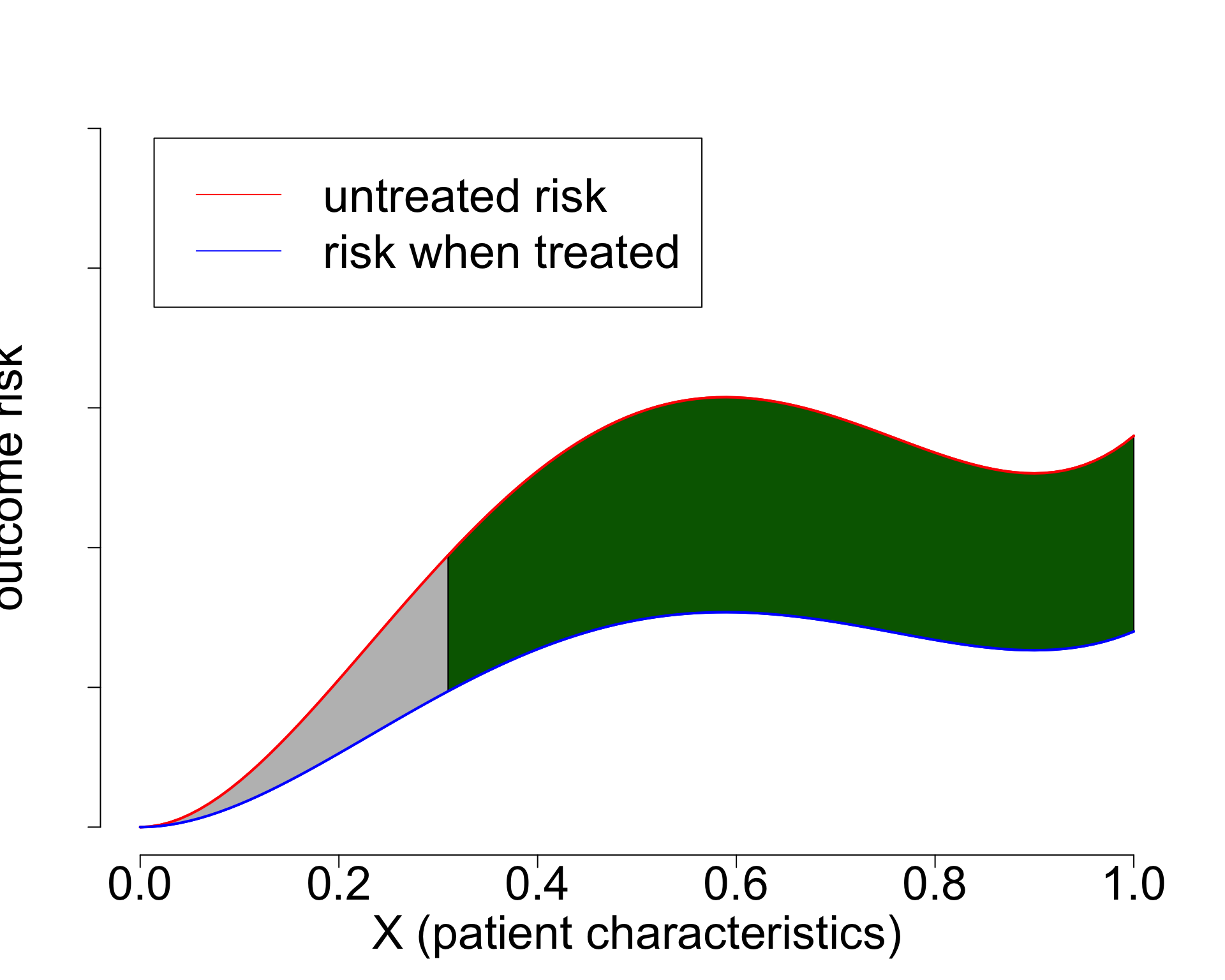
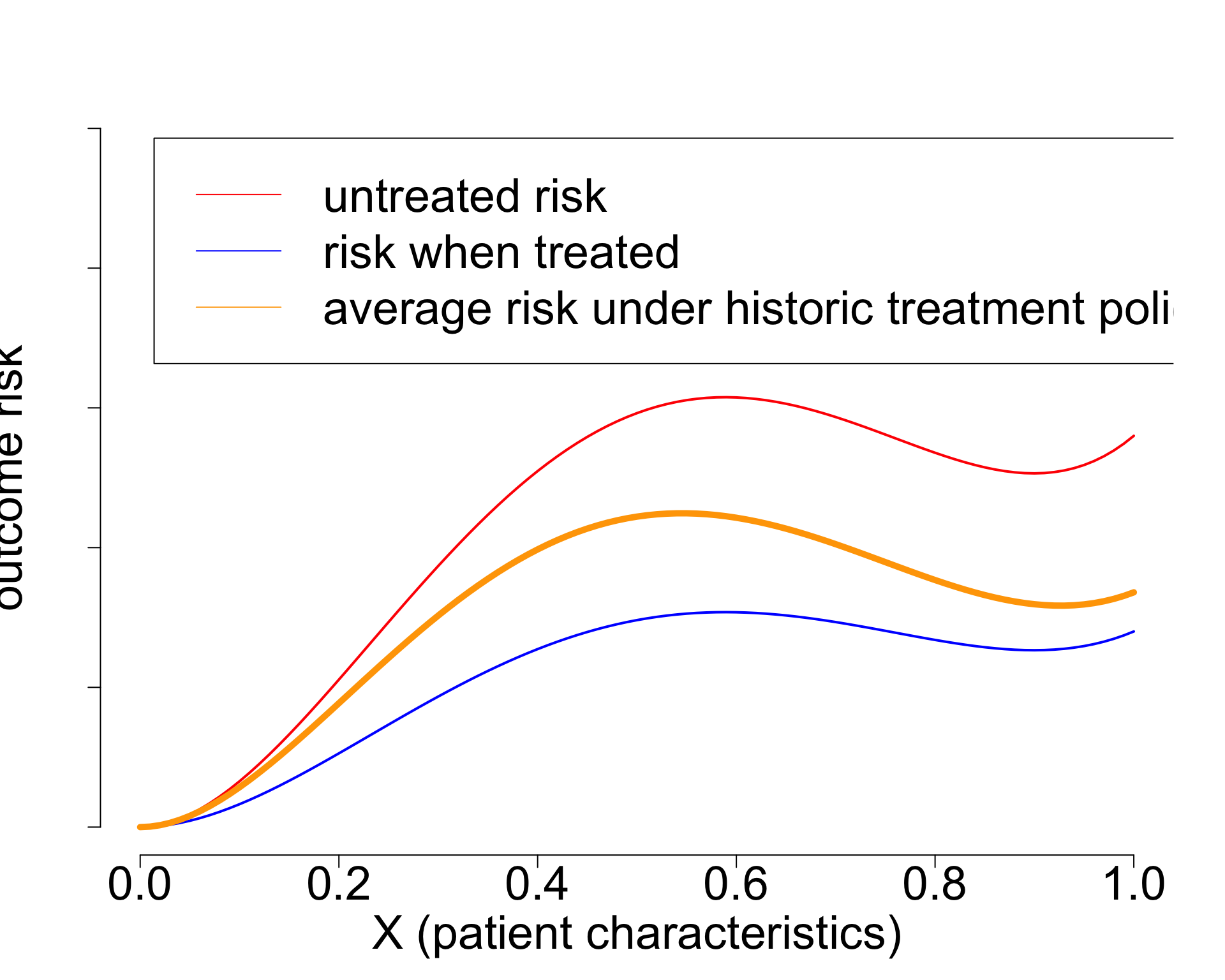
- Widely used paradigm (cardiovascular risk, chemotherapy in breast cancer, …)
- Untreated risk is a quantity of the interventional distribution (i.e. causal)
- Current risk-models: mix of treated / untreated patients (amsterdamAlgorithmsActionImproving2024?),
- or ungrounded methods (Candido dos Reis et al. 2017; Xu et al. 2021).
- Need better `causal’ methods (van Amsterdam and Ranganath 2023)
Prediction-under-intervention approaches sound great
- but come with their own assumptions and trade-offs
- do sensitivity analysis
- may not have treatment information
- may be many decision time-points, hard to formulate estimand over long time-horizon
How to proceed?
- build prediction-under-intervention model with best data + assumptions
- test policy value in historical RCT data of competing policies (e.g. current practice vs policy by new model)
- for each patient in RCT, determine recommended treatment according to policy
- if actual (randomly allocated) treatment is concordant, keep the patient
- if not, drop observation
- calculate average outcomes in the subpopulation
- policy with highest average outcomes is best
- then do a cluster RCT
Take-aways
- Prediction and causal inference come together neatly by declaring E[Y|\text{do}(T=t),X] as the estimand
- (mis)using prediction models for treatment decisions without causal thinking and evaluation is a bad idea
- deploying models for decision support is an intervention and should be evaluated as such
From algorithms to action: improving patient care requires causality (amsterdamAlgorithmsActionImproving2024?)
When accurate prediction models yield harmful sel-fulfilling prophecies (vanamsterdamWhenAccuratePrediction2024a?)
References
Candido dos Reis, Francisco J., Gordon C. Wishart, Ed M. Dicks, David Greenberg, Jem Rashbass, Marjanka K. Schmidt, Alexandra J. van den Broek, et al. 2017. “An Updated PREDICT Breast Cancer Prognostication and Treatment Benefit Prediction Model with Independent Validation.” Breast Cancer Research 19 (1): 58. https://doi.org/10/gbhgpq.
Cooper, Gregory F., Constantin F. Aliferis, Richard Ambrosino, John Aronis, Bruce G. Buchanan, Richard Caruana, Michael J. Fine, et al. 1997. “An Evaluation of Machine-Learning Methods for Predicting Pneumonia Mortality.” Artificial Intelligence in Medicine 9 (2): 107–38. https://doi.org/10.1016/S0933-3657(96)00367-3.
Hilden, Jørgen, and J. Dik F. Habbema. 1987. “Prognosis in Medicine: An Analysis of Its Meaning and rôles.” Theoretical Medicine 8 (3): 349–65. https://doi.org/10.1007/BF00489469.
van Amsterdam, Wouter A. C., and Rajesh Ranganath. 2023. “Conditional Average Treatment Effect Estimation with Marginally Constrained Models.” Journal of Causal Inference 11 (1): 20220027. https://doi.org/10.1515/jci-2022-0027.
van Amsterdam, Wouter A. C., Joost J. C. Verhoeff, Netanja I. Harlianto, Gijs A. Bartholomeus, Aahlad Manas Puli, Pim A. de Jong, Tim Leiner, Anne S. R. van Lindert, Marinus J. C. Eijkemans, and Rajesh Ranganath. 2022. “Individual Treatment Effect Estimation in the Presence of Unobserved Confounding Using Proxies: A Cohort Study in Stage III Non-Small Cell Lung Cancer.” Scientific Reports 12 (1): 5848. https://doi.org/10.1038/s41598-022-09775-9.
Xu, Zhe, Matthew Arnold, David Stevens, Stephen Kaptoge, Lisa Pennells, Michael J Sweeting, Jessica Barrett, Emanuele Di Angelantonio, and Angela M Wood. 2021. “Prediction of Cardiovascular Disease Risk Accounting for Future Initiation of Statin Treatment.” American Journal of Epidemiology, February, kwab031. https://doi.org/10/gmj9rw.
©Wouter van Amsterdam — WvanAmsterdam — wvanamsterdam.com/talks
Causality and prediction: developing and validating models for decision making Causal Data Science Special Interest Group - Utrecht Wouter van Amsterdam Department of Data Science Methods, Julius Center, University Medical Center Utrecht 2024-05-16