Causal perspectives on prediction modeling

Wouter van Amsterdam

2024-08-08

Recap: causal questions

  • questions of association are of the kind:
    • what is the probability of \(Y\) (potentially: after observing \(X\))?, e.g.:
      • what is the chance of rain tomorrow given that is was dry today?
      • what is the chance a patient with lung cancer lives more than 10% after diagnosis?
    • these hands behind your back and passively observe the world-questions
  • causal questions are of the kind:
    • how would \(Y\) change when we intervene on \(T\)?, e.g.:
      • if we would send all pregant women to the hospital for delivery, what would happen with neonatal outcomes?
      • if we start a marketing campain, by how much would our revenue increase?
    • these tell us what would happen if we changed something

What is prediction?

Examples of prediction tasks

observe an \(X\), want to know what to expect for \(Y\)

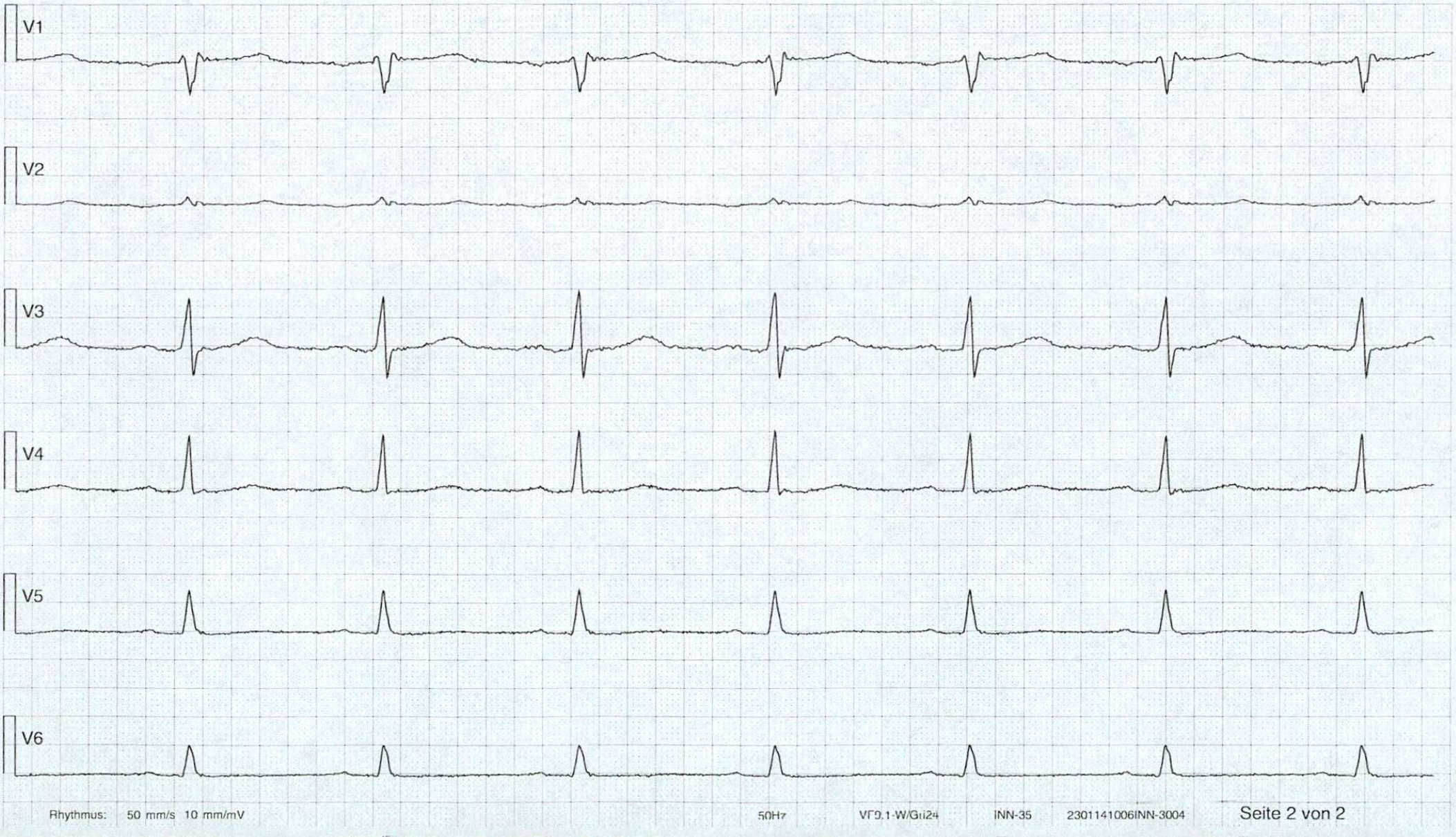
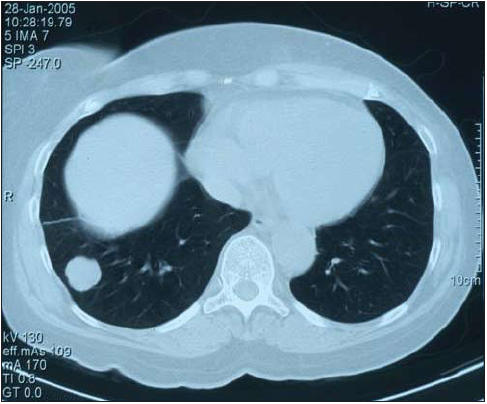
1. X = patient caughs, Y = patient has lung cancer

2. X = ECG, Y = patient has heart attack

3. X = CT-scan, Y = patient dies within 2 years

Renziehausen (2024). ECG normalized-2.jpgCoronary spasm - a cause of acute coronary syndrome with ST-segment elevation and refractory cardiogenic shock - a case report. figshare. Figure. https://doi.org/10.6084/m9.figshare.26045203.v1

M Sherigar, Jagannath; Finnegan, Joseen; McManus, Damien; F Lioe, Tong; AJ Spence, Roy (2011). CT Scan of chest showing one of the lung nodules. figshare. Figure. https://doi.org/10.6084/m9.figshare.16069.v1

Prediction: typical approach

  1. define population, find a cohort
  2. measure \(X\) at prediction baseline
  3. measure \(Y\)
    1. cross-sectional (e.g. diagnosis)
    2. longitudinal follow-up (e.g. survival)
  4. use a statistical learning technique (e.g. regression, machine learning)
  • fit model \(f\) to observed \(\{x_i,y_i\}\) with a criterion / loss function
  1. evaluate prediction performance with e.g. discrimination, calibration, \(R^2\)

Prediction: typical estimand

Let \(f\) depend on parameter \(\theta\), prediction typically aims for:

\[f_{\theta}(x) \to E[Y|X=x]\]

  • when \(Y\) is binary:
    • probability of a heart attack in 10 years, given age and cholesterol
    • probability of lung cancer, given symptoms and CT-scan
    • typical evaluation metrics:
      • discrimination: sensitivity, specificity, AUC
      • calibration

Causal inference: typical approach

  1. define target population and targeted treatment comparison
  2. run randomized controlled trial, randomizing treatment allocation (when possible)
  3. measure patient outcomes
  4. estimate parameter that summarizes average treatment effect (ATE)

typical estimand:

\[E[Y|\text{do}(T=1)] - E[Y|\text{do}(T=0)]\]

Causal inference versus prediction

prediction

  • typical estimand \(E[Y|X]\)
  • typical study: longitudinal cohort
  • typical interpretation: \(X\) predicts \(Y\)
  • primary use: know what \(Y\) to expect when observing a new \(X\) assuming no change in joint distribution

causal inference

  • typical estimand \(E[Y|\text{do}(T=1)] - E[Y|\text{do}(T=0)]\)
  • typical study: RCT (or observational causal inference study)
  • typical interpretation: causal effect of \(T\) on \(Y\)
  • primary use: know what change in \(Y\) to expect when changing the treatment policy

What do we mean with treatment policy?

A treatment policy \(\pi\) is a procedure for determining the treatment

Assuming \(T\) is binary, \(\pi\) can be:

  • \(\pi = 0.5\) (a 1/1 RCT)
  • give blood pressure pill to patients with hypertension:

\[\pi(blood pressure) = \begin{cases} 1, &blood pressure > 140mmHg\\ 0, &\text{otherwise} \end{cases}\]

  • give statins to patients with more than 10% predicted risk of heart attack:

\[\pi(X) = \begin{cases} 1, &f(X) > 0.1\\ 0, &\text{otherwise} \end{cases}\]

  • the propensity score can be seen as a (non-deterministic) treatment policy

Where can prediction and causality meet?

  1. prediction has a causal interpretation
  2. prediction does not have a causal interpretation:
    1. but is used for a causal task (e.g. treatment decision making)
    2. but predictions can be improved with causal thinking in terms of e.g.:
    • interpretability, robustness, ‘spurious correlations’, generalization, fairness, selection bias

2a. Prediction model used for a causal task

Using prediction models for decision making is often thought of as a good idea

For example:

  1. give chemotherapy to cancer patients with high predicted risk of recurrence
  2. give statins to patients with a high risk of a heart attack

TRIPOD+AI on prediction models (Collins et al. 2024)

“Their primary use is to support clinical decision making, such as … initiate treatment or lifestyle changes.”

This may lead to bad situations when:

  1. ignoring the treatments patients may have had during training / validation of prediction model
  2. only considering measures of predictive accuracy as sufficient evidence for safe deployment

When accurate prediction models yield harmful self-fulfilling prophecies

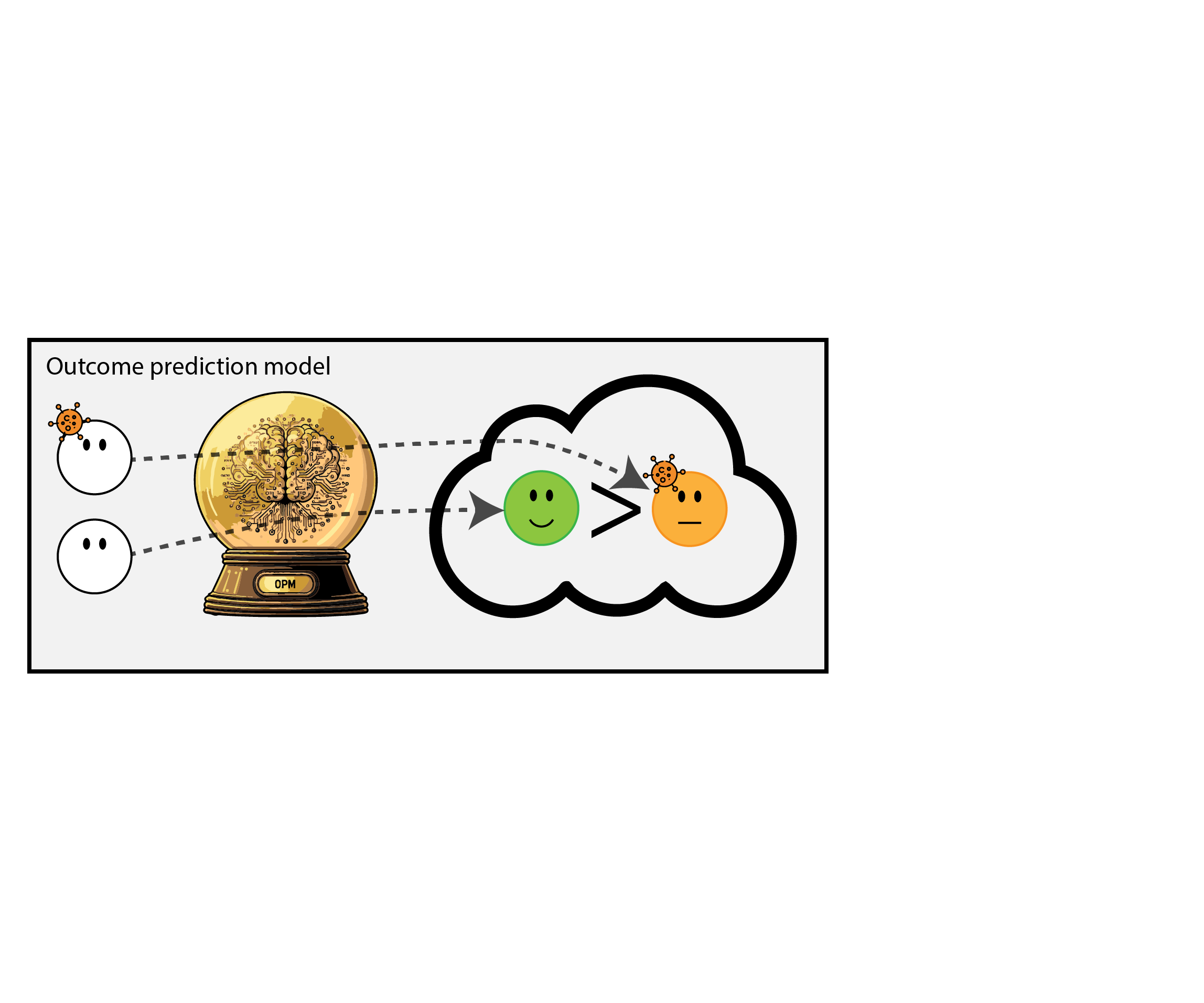
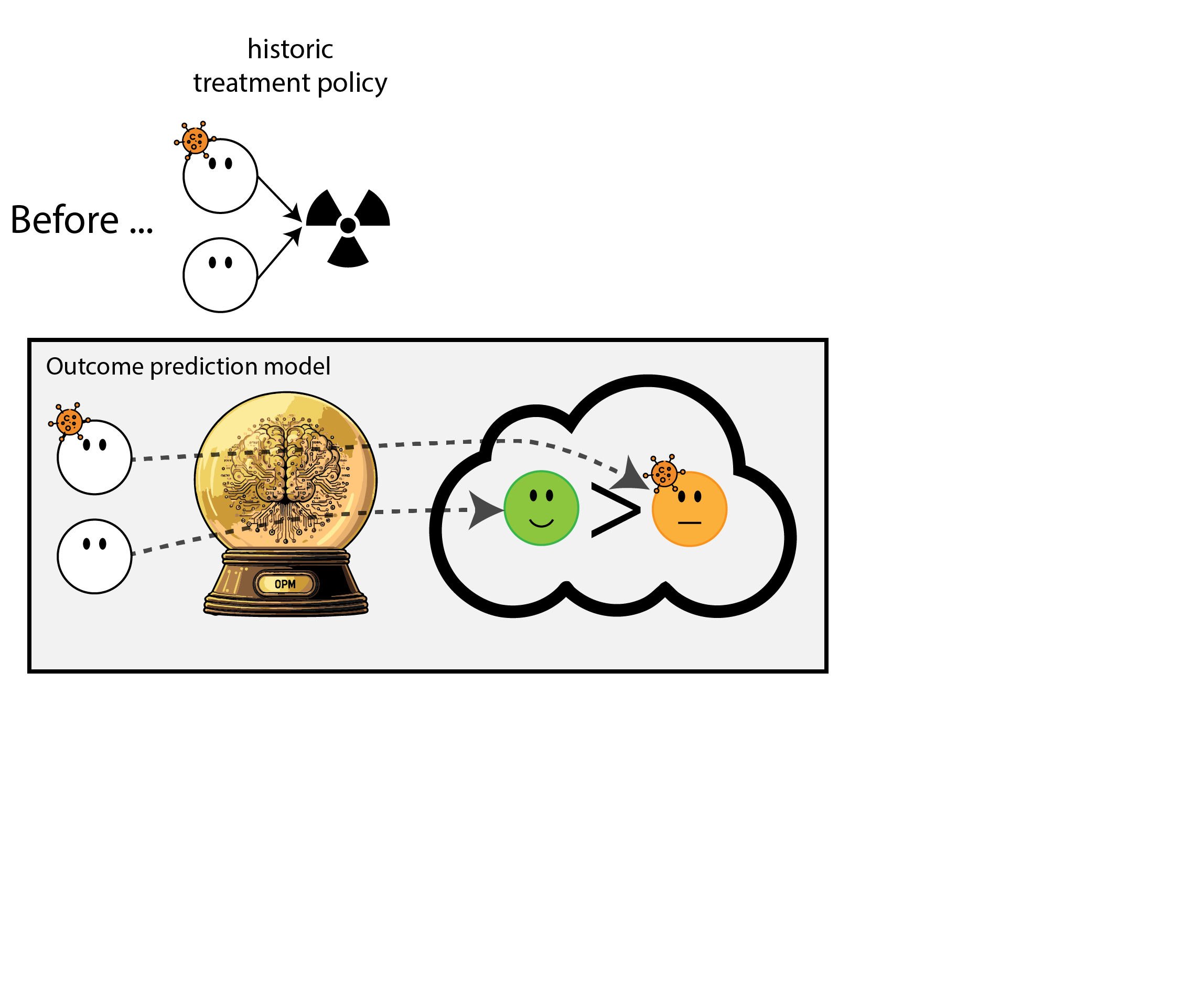
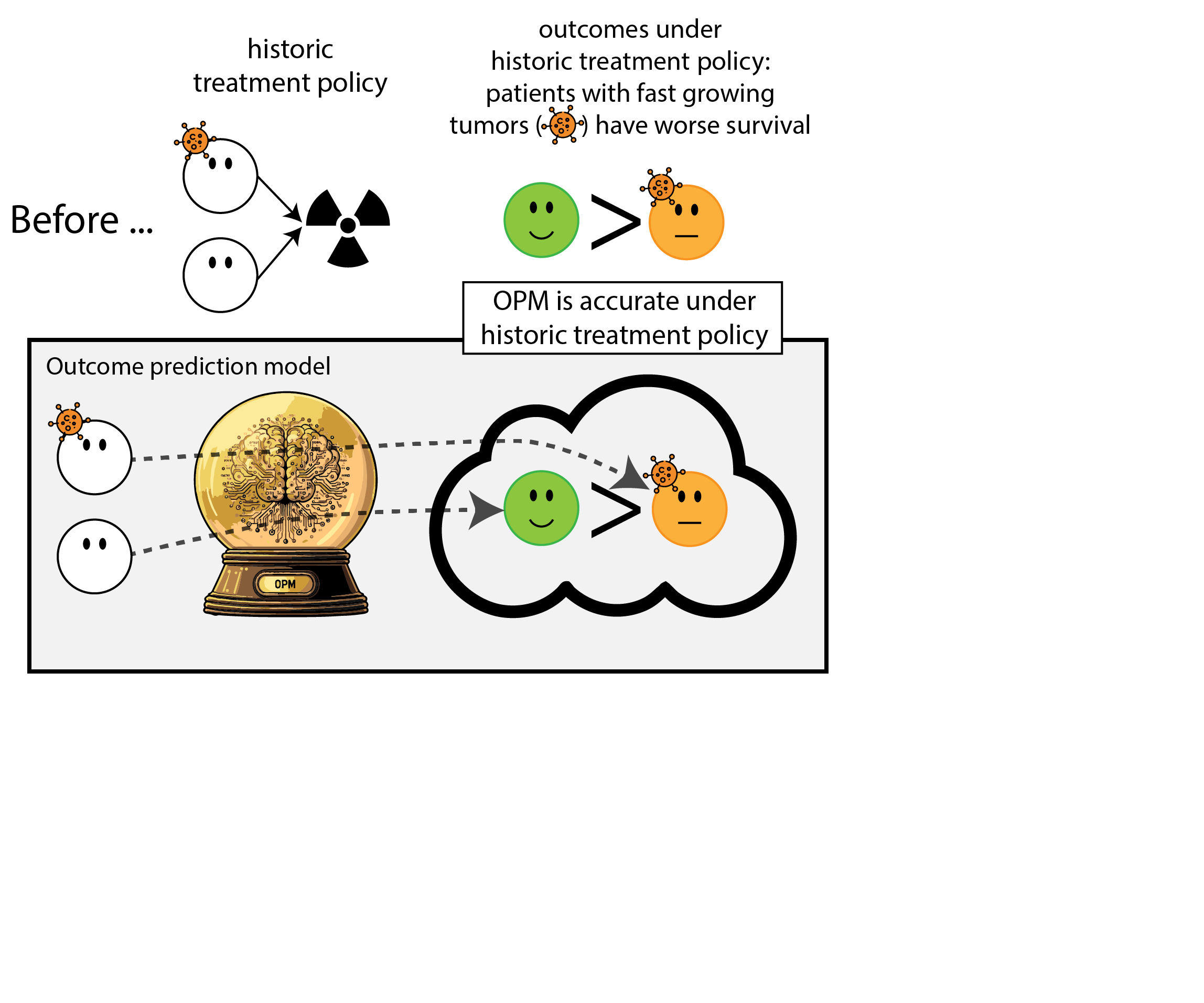
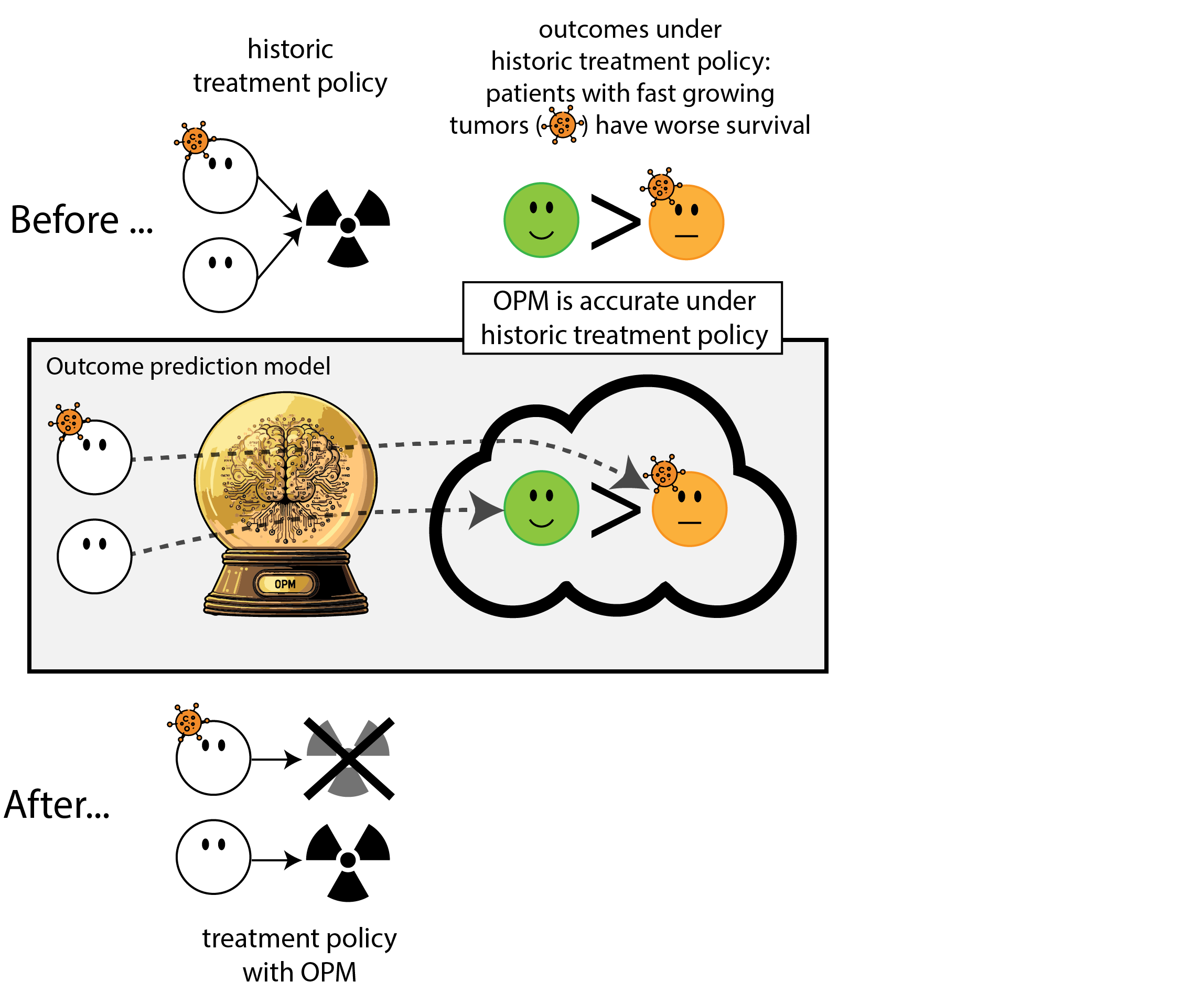
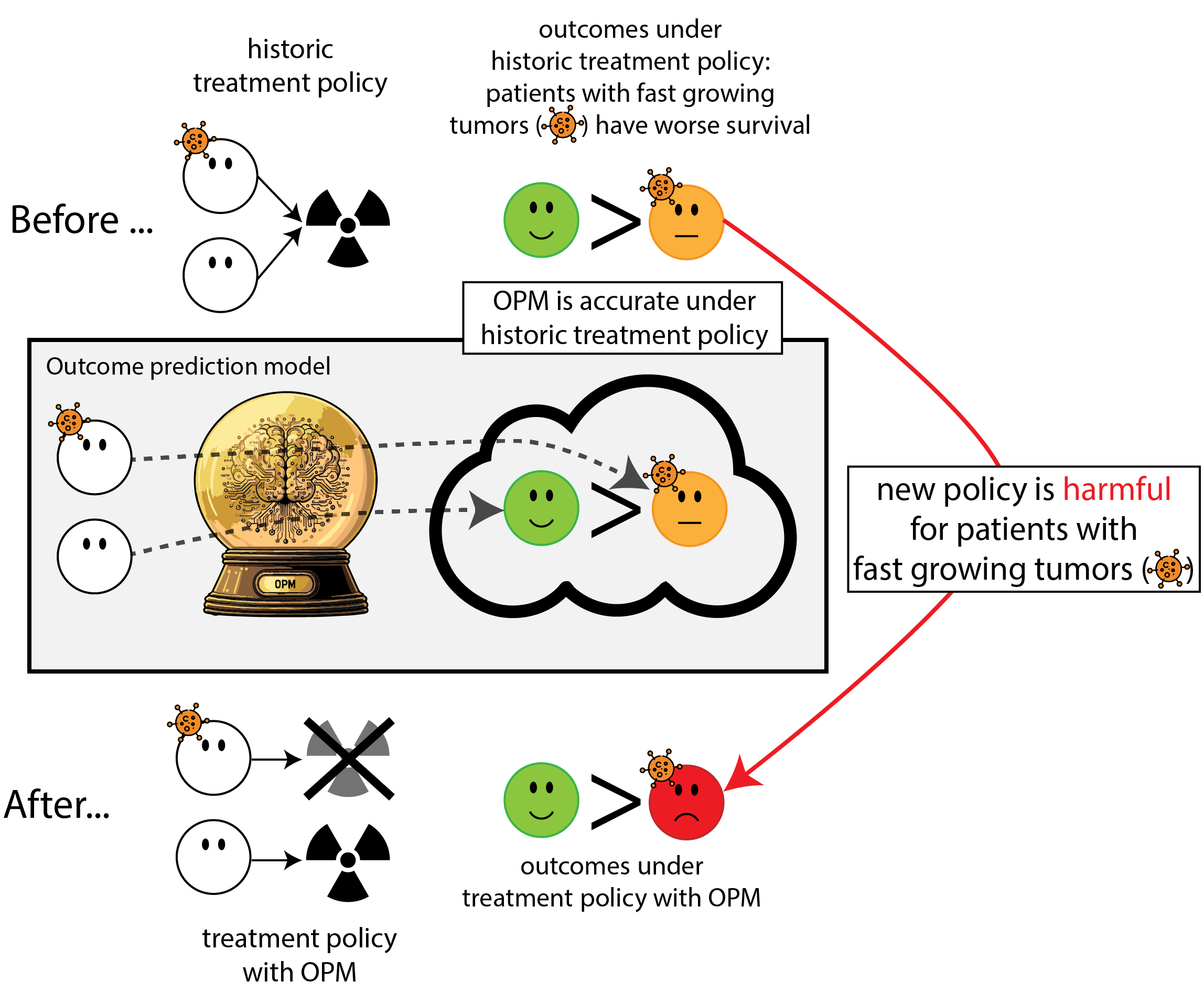
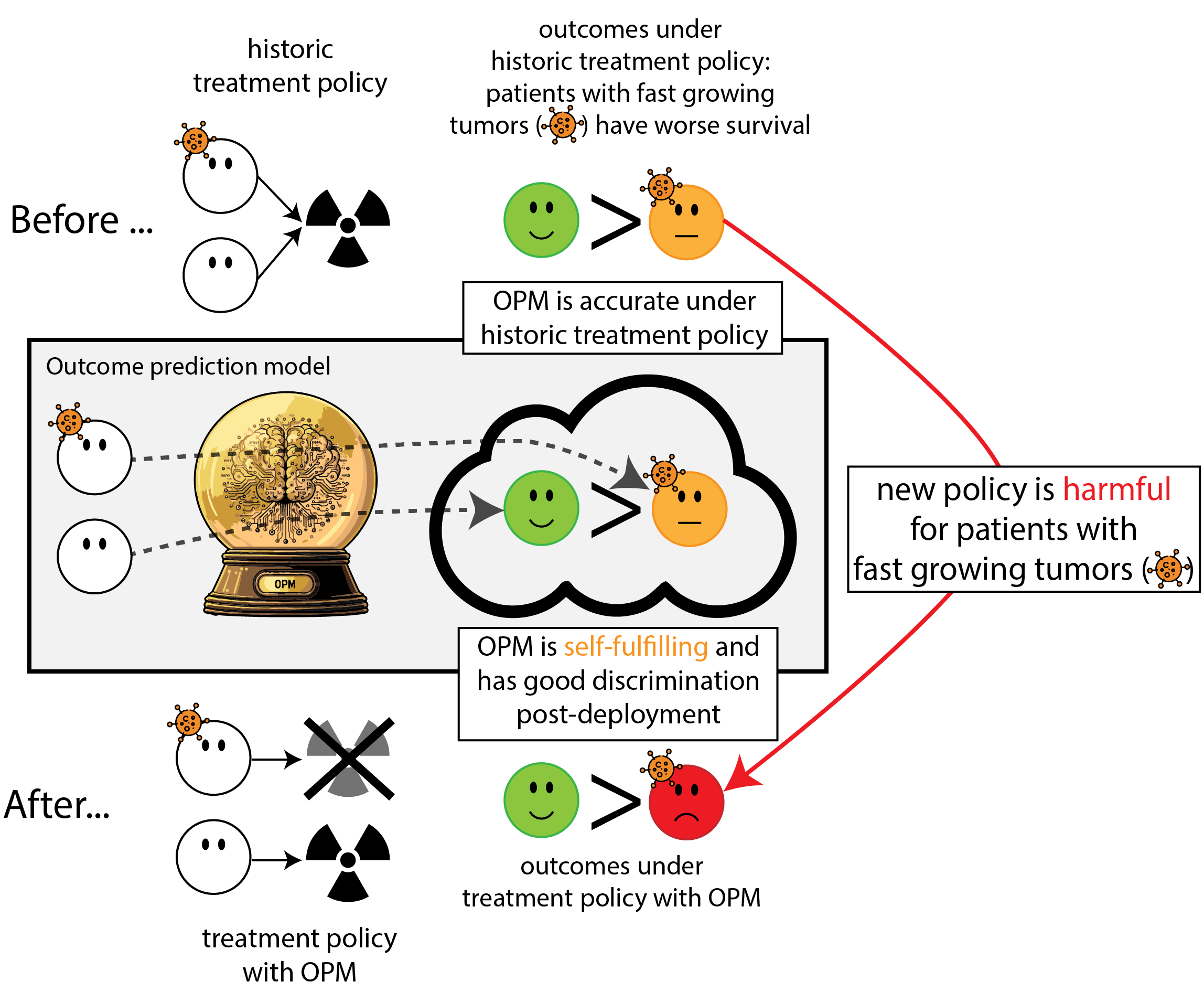
Building models for decision support without regards for the historic treatment policy is a bad idea

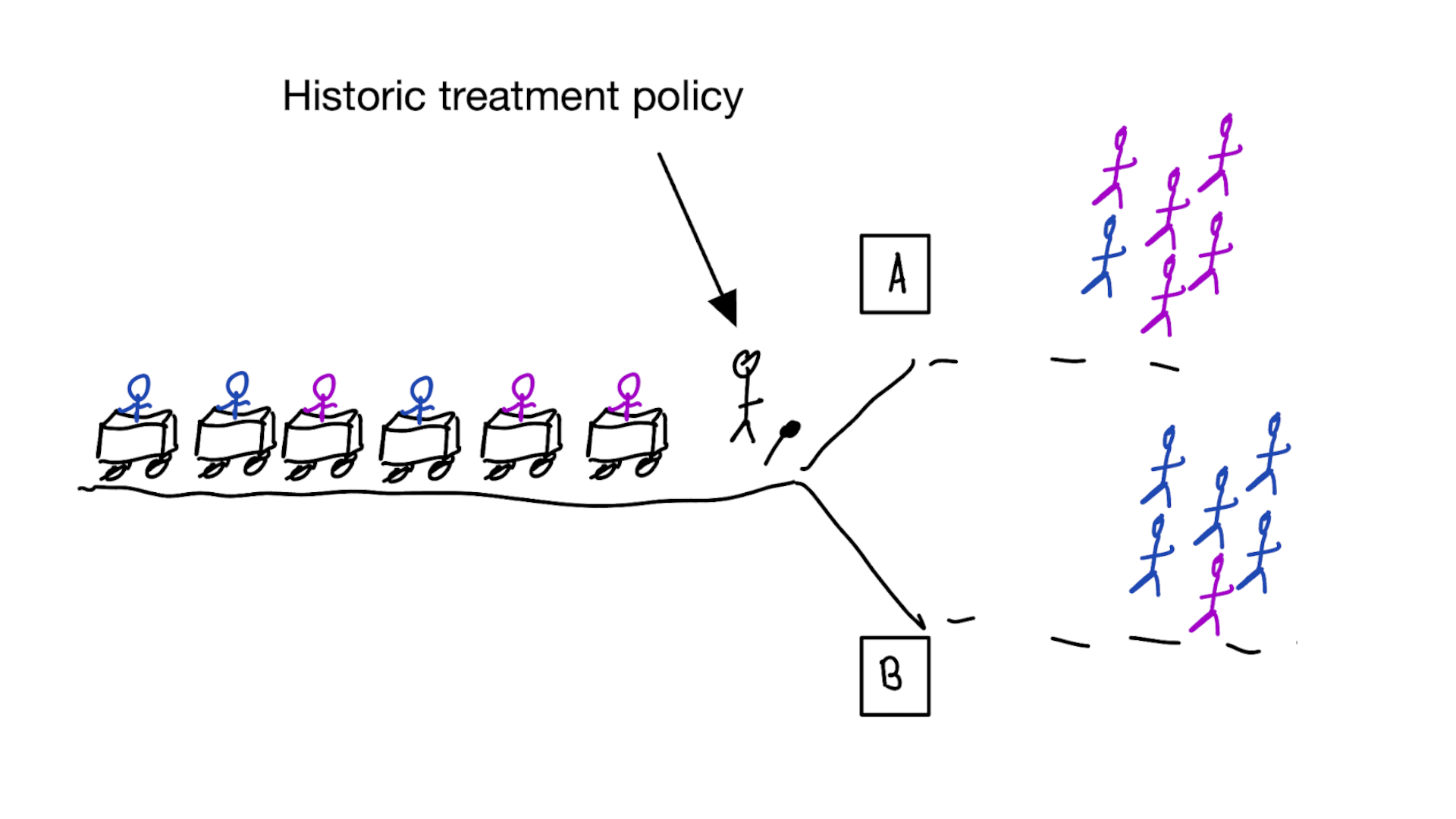
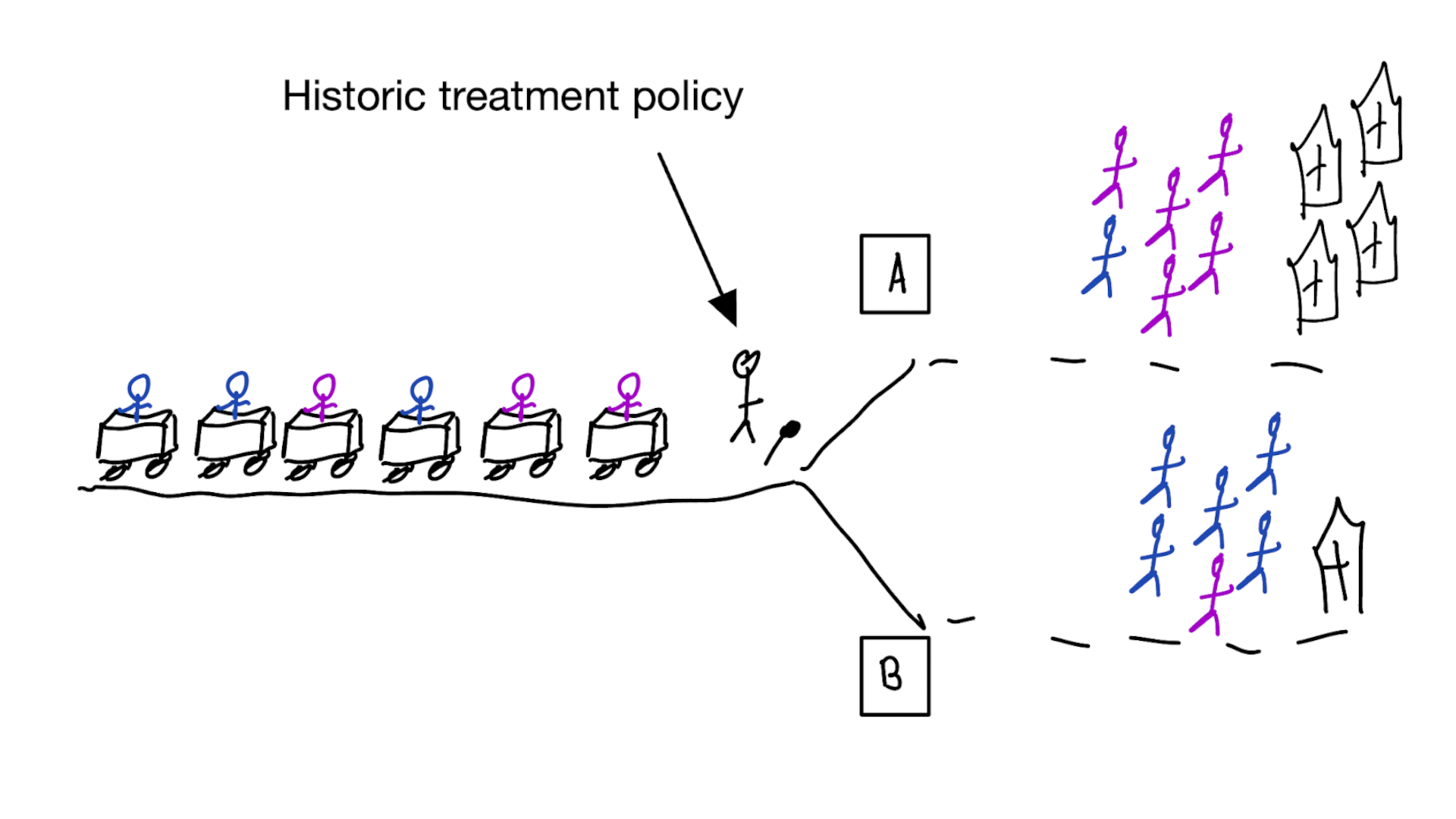
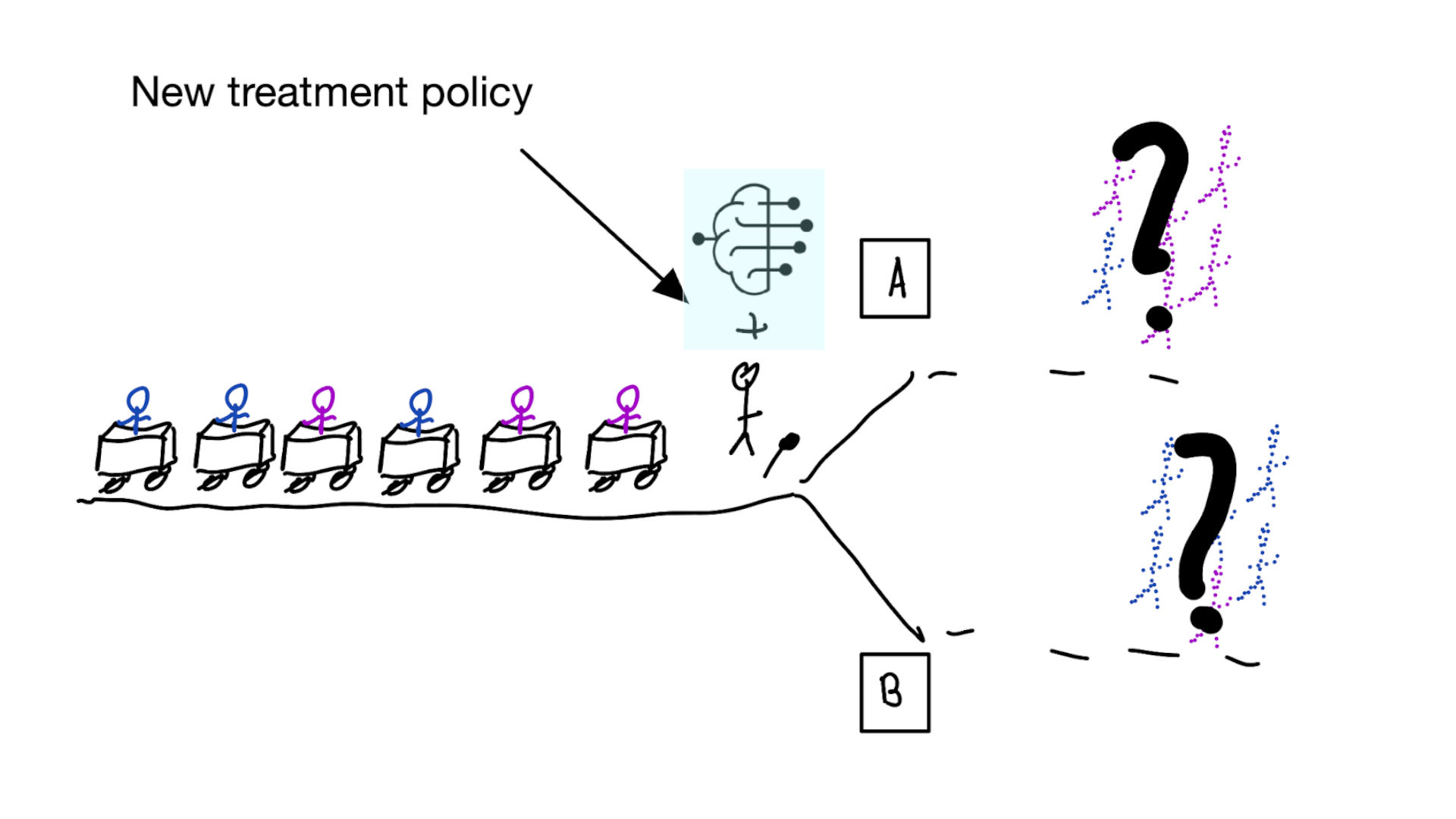
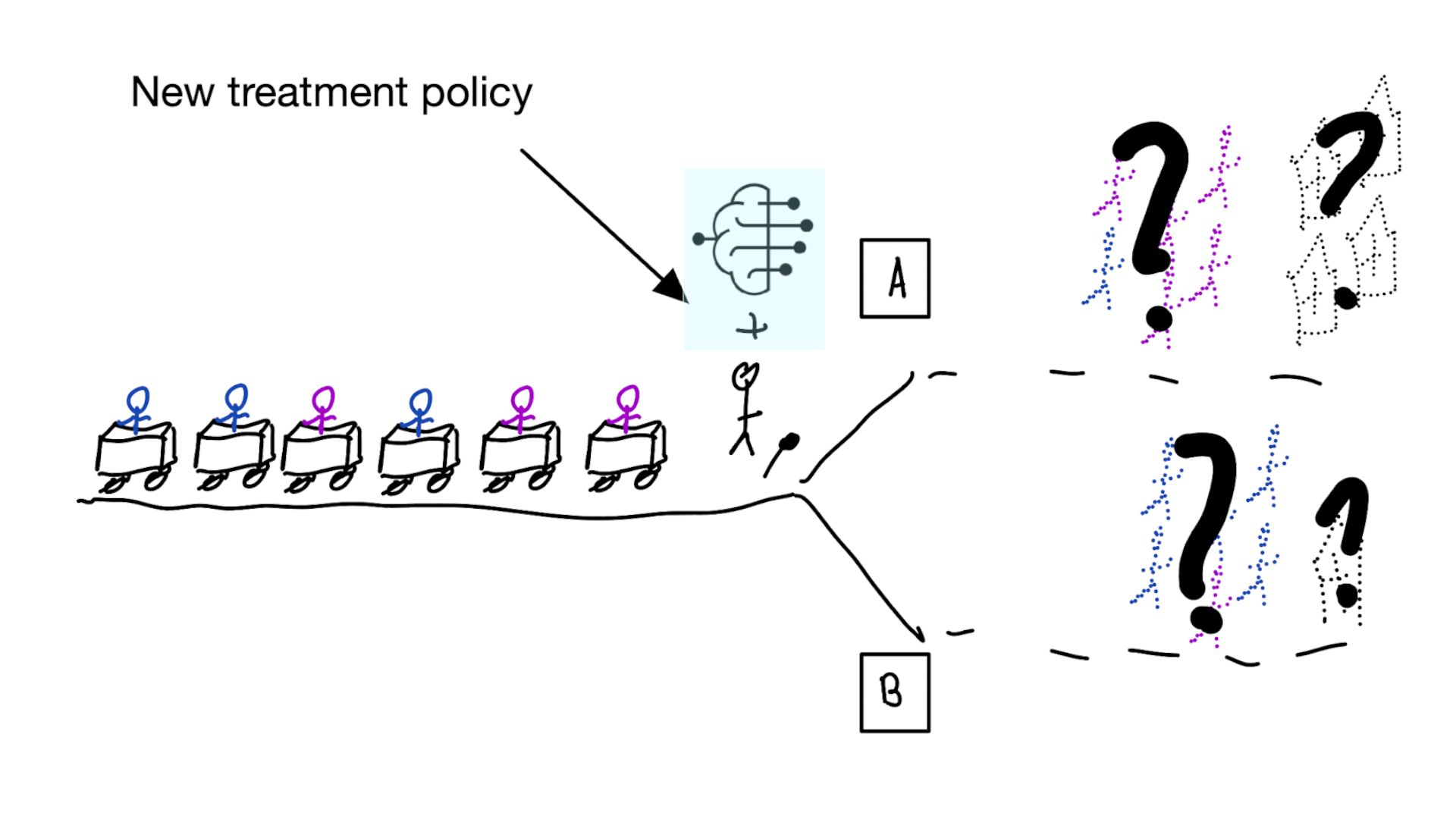
The question is not “is my model accurate before / after deployment”,

but did deploying the model improve patient outcomes?

Treatment-naive prediction models

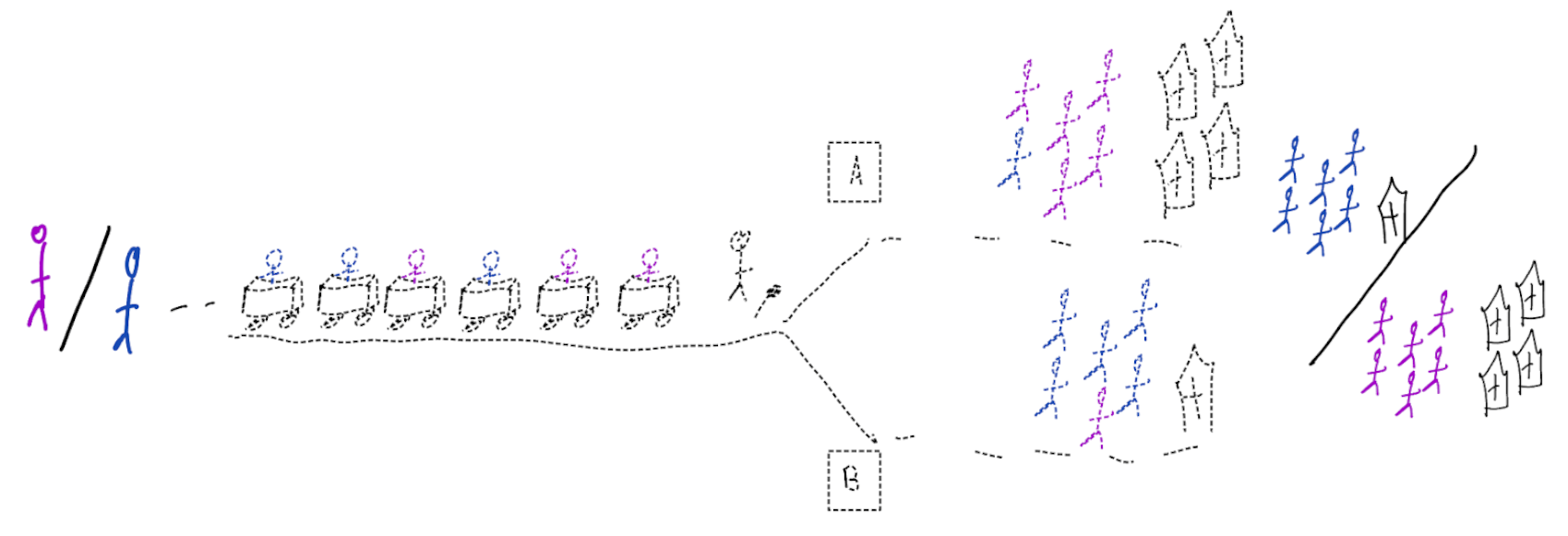
\[\begin{align} E[Y|X] \class{fragment}{= E[E_{t~\sim \pi_0(X)}[Y|X,t]]} \end{align}\]

Is this obvious?

Bigger data does not protect against harmful prediction models

More flexible models do not protect against harmful prediction models

What to do?

What to do?

  1. Evaluate policy change (cluster randomized controlled trial)
  2. Build models that are likely to have value for decision making

How to evaluate the effect of a new treatment policy?

Deploying a model is an intervention that changes the way treatment decisions are made

How do we learn about the effect of an intervention?

With causal inference!

  • for using a decision support model, the unit of intervention is usually the doctor
  • randomly assign doctors to have access to the model or not
  • measure differences in treatment decisions and patient outcomes
  • this called a cluster RCT
  • if using model improves outcomes, use that one

Using cluster RCTs to evaluated models for decision making is not a new idea (Cooper et al. 1997)

“As one possibility, suppose that a trial is performed in which clinicians are randomized either to have or not to have access to such a decision aid in making decisions about where to treat patients who present with pneumonia.”

What we don’t learn

was the model predicting anything sensible?

What if we cannot do this (cluster randomized) trial?

Off-policy evaluation

  1. have historic RCT data, want to evaluate new policy \(\pi_1\)
    • target distribution \(p(t|x)=\pi_1(x)\)
    • observed distribution \(q(t|x) = 0.5\)
    • note: when \(\pi_1(x)\) is deterministic (e.g. give the treatment when \(f(x) > 0.1\)), we get the following:
      1. when randomized treatment is concordant with \(\pi_1\), keep the patient (weight = 1), otherwise, remove from the data (weight = 0)
      2. calculate average outcomes in the kept patients
    • this way, multiple alternative policies may be evaluated
  2. have historic observational data, want to evaluate new policy \(\pi_1\):
    • target distribution \(p(t|x)=\pi_1(x)\)
    • observed distribution \(q(t|x) = \pi_0(x)\)
    • we need to estimate \(q\) (i.e. the propensity score), this procedure relies on the standard causal inference assumptions (no confounding, positivity)
    • use importance sampling to estimate the expected value of \(Y\) under \(\pi_1\) from the observed data

How to build prediction models for decision support?

1. Prediction has a causal interpretation

What can we mean with predictions having a causal interpretation?

Let \(f: \mathbb{X} \to \mathbb{Y}\) be a prediction model for outcome \(Y\) using features \(X\)

  1. \(X\) is an ancestor of \(Y\) (\(X=\{z_1,z_2,z_3\}\))
  2. \(X\) is a direct cause of \(Y\) (\(X=\{z_1,z_2\}\))
  3. \(f: \mathbb{X} \to \mathbb{Y}\) describes the causal effect of \(X\) on \(Y\) (\(X=\{z_1\}\)), i.e.:

\[f(x) = E[Y|\text{do}(X=x)]\]

  1. \(f: \mathbb{T} \times \mathbb{X} \to \mathbb{Y}\) describes the causal effect of \(T\) on \(Y\) conditional on \(X\) (\(T=\{z_1\},X=\{z_2,z_3,w\}\):

\[f(t,x) = E[Y|\text{do}(T=t),X=x]\]

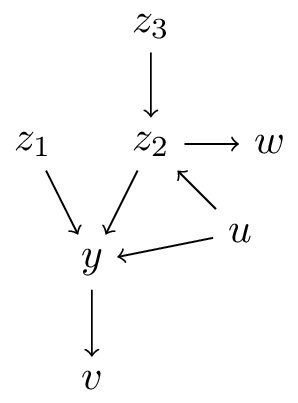
interpretation 3. all covariates are causal

Let \(f: \mathbb{X} \to \mathbb{Y}\) be a prediction model for outcome \(Y\) using features \(X\)

\[f(x) = E[Y|\text{do}(X=x)]\]

  • this is almost never true (i.e. back-door rule holds for all variables)
  • too often this is assumed / interpreted this way (table 2 fallacy in health care literature)

Example of table 2 fallacy when mis-using Qrisk

Qrisk3: a risk prediction model for cardiovascular events in the coming 10-years. Widely used in the United Kingdom for deciding which patients should get statins

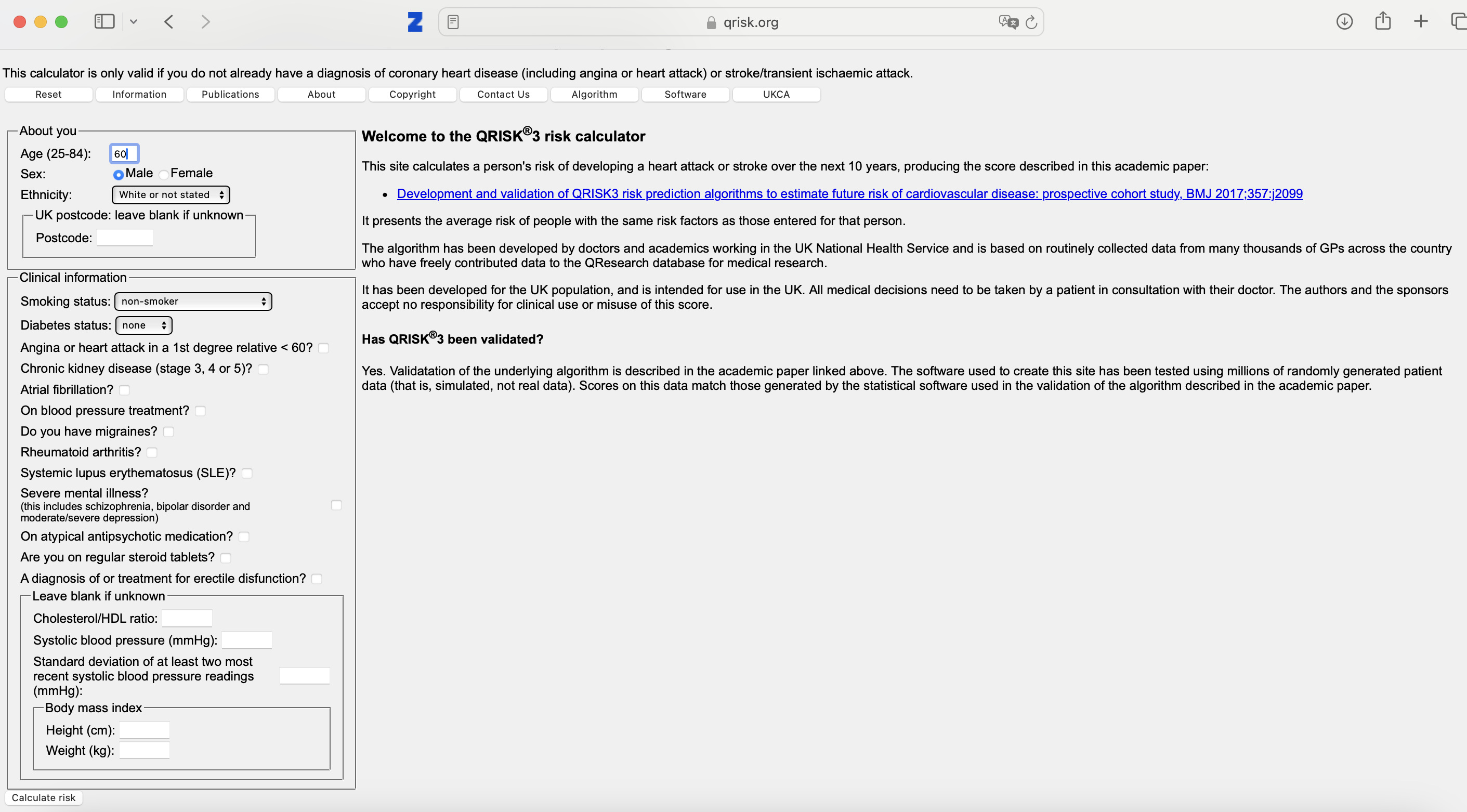
Qrisk3 - risks:

can go wrong when:

  • e.g. fill in current length and weight
    • reduce weight by 5 kgs
    • interpret difference as ‘effect of weight loss’
  • check or un-check blood pressure medication
    • observe that with blood pressure medication, risk is higher

What else could go wrong?

  • Qrisk3 states it is validated, but validated for what?
  • Qrisk3 is validated for non-use!

interpretation 4. some covariates are causal

or: prediction-under-intervention

\[f(t,x) = E[Y|\text{do}(T=t),X=x]\]

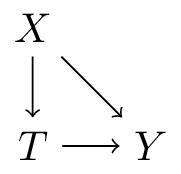
  • interpretation: what is the expected value of \(Y\) if we were to assign treatment \(t\) by intervention, given that we know \(X=x\) in this patient

using treatment naive prediction models for decision support

prediction-under-intervention

Estimand for prediction-under-intervention models

What is the estimand?

  • prediction: \(E[Y|X]\)
  • average treatment effect: \(E[Y|\text{do}(T=1)] - E[Y|\text{do}(T=0)]\)
  • conditional average treatment effect: \(E[Y|\text{do}(T=1),X] - E[Y|\text{do}(T=0),X]\)
  • prediction-under-intervention: \(E[Y|\text{do}(T=t),X]\)

note:

  • from prediction-under-intervention models, the CATE can be derived
  • in these models and the CATE: \(T\) has a causal interpretation, \(X\) does not!
    • i.e. \(X\) does not cause the effect of treatment to be different

Developing prediction-under-intervention models

Evaluation of prediction-under-intervention models

  • prediction accuracy can be tested in RCTs, or in observational data with specialized methods accounting for confounding (e.g. Keogh and van Geloven 2024)
  • in confounded observational data, typical metrics (e.g. AUC or calibration) are not sufficient as we want to predict well in data from other distribution than observed data (i.e. other treatment decisions)
  • a new policy can be evaluated in historic RCTs (e.g. Karmali et al. 2018)
  • ultimate test is cluster RCT
  • if not perfect, likely a better recipe than treatment-naive models

2b. improving non-causal prediction models with causality

  • interpretability
  • robustness / ‘spurious correlations’ / generalization
  • fairness
  • selection bias

Interpretability

  • end-users (e.g. doctors) often want to understand why a prediction model returns a certain prediction
  • this has two possible interpretations:
    1. explain the model (i.e. the computations)
    2. explain the world (i.e. why is this patient at high risk of a certain outcome)
    1. often has a causal connotation, though achieving this is may be unfeasible as you need causal assumptions on all covariates (rember table 2 fallacy)

Robustness / spurious correlations / generalization

  • prediction models are developed in some data, but are intended to be used elsewhere (in location, time, other)
  • in causal language, shifts in distributions can be denoted as interventions on specific nodes
  • prediction models that include (direct) causes may be more robust to changes as the chain between \(X\) and \(Y\) is shorter
  • some machine learning algorithms like deep learning are very good at detecting ‘background’ signals, e.g.:
    • detect the scanner type from a CT-scanner
      • if hospital A has scanner type 1 and hospital B has scanner type 2
      • and the outcome rates differ between the hospitals, models may (mis)use the scanner type to predict the outcome
      • what will the model predict in hospital C? or when A or B buy a scanner of different type?
    • may be preventable with causality

Fairness

  • in the historic distribution, outcomes may be affected by unequal treatment of certain demographic groups
  • instead of perpetuating inequities, we may want to design models that diminish them
  • this means intervening in the distribution (= a causal task)
  • causality has a strong vocabulary for formalizing fairness
  • actually achieving fairness is highly non-trivial, not in the least part due to unclear definitions
  • chosing to not include sensitive attributes in a prediction model is often not gauranteed to improve fairness

Selection bias

  • have samples from some selected subpopulation
    • university hospital
    • older men
  • want to generalize to another subpopulation
    • general practitioner
    • younger women
  • use DAGs to express the difference between source and target population
  • calculate e.g. expected performance on target population with techniques like importance sampling

Wrap-up

  • predictions can have causal interpretations
  • prediction-under-intervention: causal with respect to treatment (not covariates)
  • mis-use of non-causal models for causal tasks (e.g. prediction model for treatment decisions) is perilous
    • always think about the policy change and its effect on outcomes
  • evaluate policy changes with cluster RCTs, or historic RCTs and importance sampling
  • causal thinking may improve other aspects of non-causal prediction models such as robustness, fairness, generalization

Proof of importance sampling unbiasedness

assuming \(x\) is discrete, otherwise replace sums with integrals for continuous \(x\)

want to compute the expected value of \(g(x)\) over distribution \(p\), but we have samples from another distribution \(x \sim q\)

\[E_{x \sim q} \left[ \frac{p(x)}{q(x)} g(x) \right] = \sum_x q(x) \left( \frac{p(x)}{q(x)} g(x) \right) = \sum_x p(x) g(x) = E_{x \sim p} \left[g(x) \right]\]

this assumes \(q(x)>0\) whenever \(p(x)>0\) for the ratio \(p/q\) to be defined

References

Alaa, Ahmed M., Deepti Gurdasani, Adrian L. Harris, Jem Rashbass, and Mihaela van der Schaar. 2021. “Machine Learning to Guide the Use of Adjuvant Therapies for Breast Cancer.” Nature Machine Intelligence, June, 1–11. https://doi.org/10/gk6bh7.
Amsterdam, Wouter A. C. van, and Rajesh Ranganath. 2023. “Conditional Average Treatment Effect Estimation with Marginally Constrained Models.” Journal of Causal Inference 11 (1): 20220027. https://doi.org/10.1515/jci-2022-0027.
Amsterdam, Wouter A. C. van, Joost J. C. Verhoeff, Netanja I. Harlianto, Gijs A. Bartholomeus, Aahlad Manas Puli, Pim A. de Jong, Tim Leiner, Anne S. R. van Lindert, Marinus J. C. Eijkemans, and Rajesh Ranganath. 2022. “Individual Treatment Effect Estimation in the Presence of Unobserved Confounding Using Proxies: A Cohort Study in Stage III Non-Small Cell Lung Cancer.” Scientific Reports 12 (1, 1): 5848. https://doi.org/10.1038/s41598-022-09775-9.
Candido dos Reis, Francisco J., Gordon C. Wishart, Ed M. Dicks, David Greenberg, Jem Rashbass, Marjanka K. Schmidt, Alexandra J. van den Broek, et al. 2017. “An Updated PREDICT Breast Cancer Prognostication and Treatment Benefit Prediction Model with Independent Validation.” Breast Cancer Research 19 (1): 58. https://doi.org/10/gbhgpq.
Collins, Gary S., Karel G. M. Moons, Paula Dhiman, Richard D. Riley, Andrew L. Beam, Ben Van Calster, Marzyeh Ghassemi, et al. 2024. “TRIPOD+AI Statement: Updated Guidance for Reporting Clinical Prediction Models That Use Regression or Machine Learning Methods.” BMJ 385 (April): e078378. https://doi.org/10.1136/bmj-2023-078378.
Cooper, Gregory F., Constantin F. Aliferis, Richard Ambrosino, John Aronis, Bruce G. Buchanan, Richard Caruana, Michael J. Fine, et al. 1997. “An Evaluation of Machine-Learning Methods for Predicting Pneumonia Mortality.” Artificial Intelligence in Medicine 9 (2): 107–38. https://doi.org/10.1016/S0933-3657(96)00367-3.
Hartford, Jason, Greg Lewis, Kevin Leyton-Brown, and Matt Taddy. 2017. “Deep IV: A Flexible Approach for Counterfactual Prediction.” In International Conference on Machine Learning, 1414–23. PMLR. https://proceedings.mlr.press/v70/hartford17a.html.
Karmali, Kunal N., Donald M. Lloyd-Jones, Joep van der Leeuw, David C. Goff Jr, Salim Yusuf, Alberto Zanchetti, Paul Glasziou, et al. 2018. “Blood Pressure-Lowering Treatment Strategies Based on Cardiovascular Risk Versus Blood Pressure: A Meta-Analysis of Individual Participant Data.” PLOS Medicine 15 (3): e1002538. https://doi.org/10.1371/journal.pmed.1002538.
Keogh, Ruth H., and Nan van Geloven. 2024. “Prediction Under Interventions: Evaluation of Counterfactual Performance Using Longitudinal Observational Data.” January 10, 2024. https://doi.org/10.48550/arXiv.2304.10005.
Miao, Wang, Zhi Geng, and Eric J Tchetgen Tchetgen. 2018. “Identifying Causal Effects with Proxy Variables of an Unmeasured Confounder.” Biometrika 105 (4): 987–93. https://doi.org/10.1093/biomet/asy038.
Puli, Aahlad Manas, and Rajesh Ranganath. 2021. “General Control Functions for Causal Effect Estimation from Instrumental Variables.” http://arxiv.org/abs/1907.03451.
Wald, Abraham. 1940. “The Fitting of Straight Lines If Both Variables Are Subject to Error.” The Annals of Mathematical Statistics 11 (3): 284–300. https://doi.org/10.1214/aoms/1177731868.