Adjustment Sets and Approaches - and limitations / critiques

Wouter van Amsterdam

2026-07-07

Adjustment sets and approaches

How to find adjustment sets?

  • adjustment sets:
    • the back-door criterion states that any set \(Z\) that blocks all backdoor paths from \(X\) to \(Y\) is a sufficient adjustment set for causal effect estimation of \(P(Y|\text{do}(X))\) using the backdoor formula.
    • how do we find these sufficient sets?
    • what if there are multiple?
  • adjustment: how to do this?
    • stratification
    • what is regression adjustment?
    • T-learner vs S-learner

Valid adjustment sets

dag
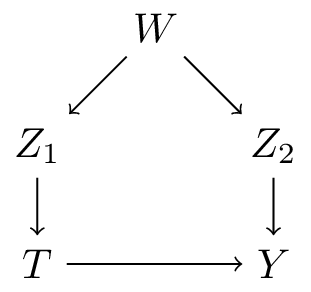
  • in general:
    • \(PA_T\) (the direct parents of treatment \(T\): \(Z_1\)) are a valid adjustment set
    • \(PA_Y\) (the direct parents of outcome \(Y\): \(Z_2\)) are a valid adjustment set
  • in this case:
    • \(W\) is also a valid adjustment set

Valid adjustment sets: picking one

  • websites like dagitty.net and causalfusion.net provide user-friendly interfaces for creating and exporting DAGs, in addition:
    • valid adjustment sets (if they exist)
    • testable conditional independencies

daggity.net

causalfusion.net

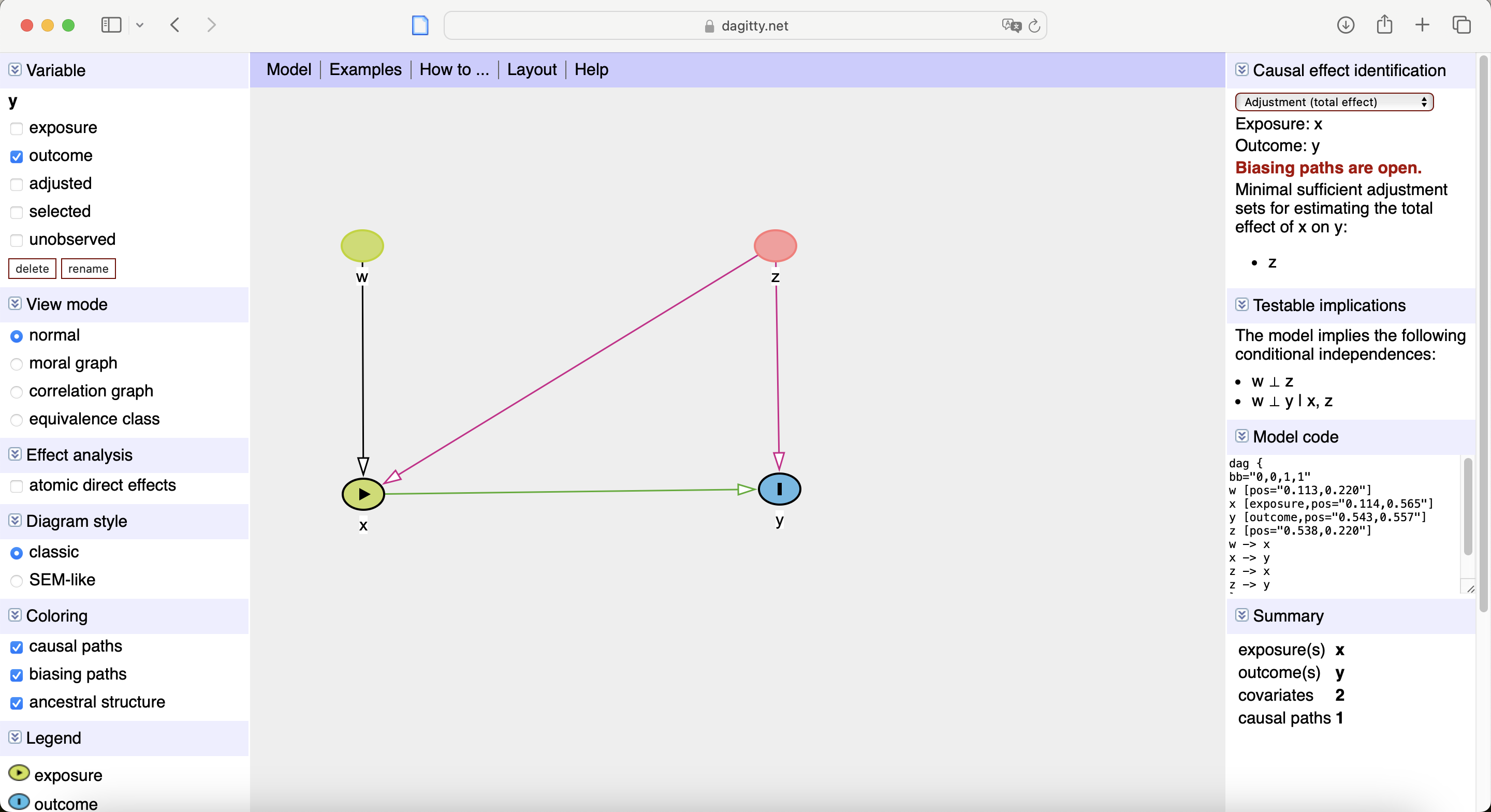
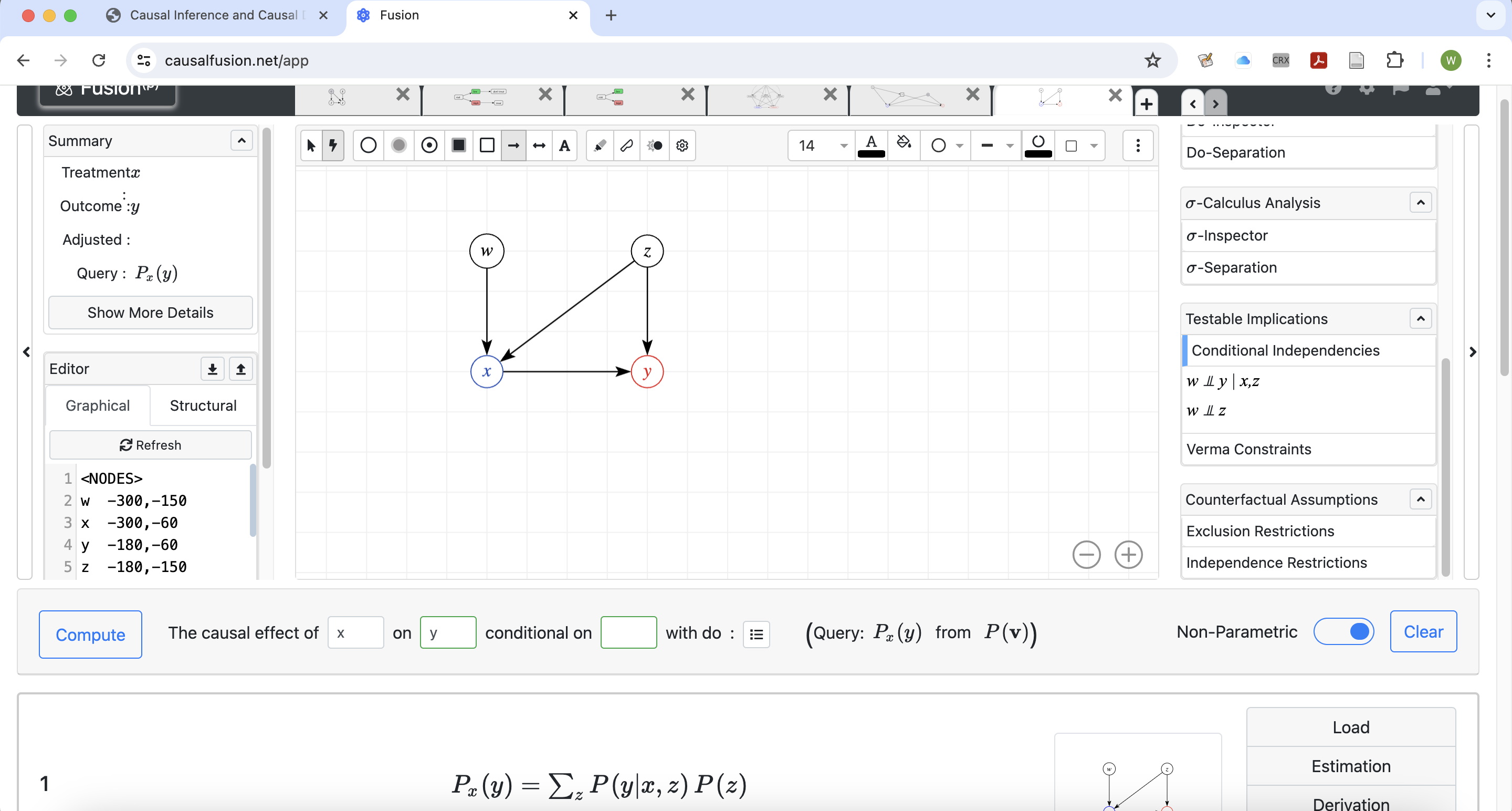
How to do adjustment

What not to do

  1. do univariable pre-screening against outcome (and / or treatment)
  • this should maybe never be done
  • especially not in the context of causal inference

Adjustment formula

\[P(y|\text{do}(x)) = \sum_z P(y|x,z)P(z)\]

  • entails summing over all possible values of \(Z\)
  • say \(Z\) is 5 categorical variables with each 3 categories, this means \(4^5=1024\) estimates of:
    • \(P(y|x,z)\) for each value of \(x\)
  • what if \(Z\) is continuous?
  • in practice, researchers often rely on smoothness assumptions (e.g. regression) to estimate \(P(Y|x,z)\) with a parametric model
  • this assumption can be based on substantive causal knowledge, but often seems inspired rather pragmatism or necessity
  • misspecification of this estimator leads to biased results (even if you observed all the confounders)

Target queries

  • up to now we’ve worked exclusively with \(P(y|\text{do}(t))\): the probability of observing outcome \(y\) when setting treatment \(T\) to \(t\)
  • this is not typically what is of most interest, say there are two treatment options \(T \in \{0,1\}\) (control and ‘treatment’)
    1. average treatment effect \[\text{ATE} = E[y|\text{do}(t=1)] - E[y|\text{do}(t=0)]\]
    2. conditional average treatment effect \[\text{CATE} = E[y|\text{do}(t=1),w] - E[y|\text{do}(t=0),w]\]
    3. prediction-under-intervention \(P(y|\text{do}(t),w)\) (more on this on day 4)
  • these can be computed from \(P(y|\text{do}(t),w)\)

The simplest case: linear regression

  • assume the following structural causal model (\(z\) is confounder, \(u\) is exogenous noise): \[f_y(t,z,u) = \beta_t t + \beta_z z + \beta_u u\]

  • then: \[\begin{align} \text{ATE} &= E[Y|\text{do}(t=1)] - E[Y|\text{do}(t=0)] \\ &\class{fragment}{= E_{z,u}[\beta_t * 1+ \beta_z z + \beta_u u] - E_{z,u}[\beta_t * 0 + \beta_z z + \beta_u u]} \\ &\class{fragment}{= \beta_t + E_{z,u}[\beta_z z + \beta_u u] - E_{z,u}[\beta_z z + \beta_u u]} \\ &\class{fragment}{= \beta_t} \end{align}\]

  • i.e. the ATE collapses to the the regression parameter \(\beta_t\) in a linear regression model of \(y\) on \(t,z\)

Binary outcome: logistic regression

  • researchers make the following substantive assumption: the log-odds of the outcome is linear in the treatment and confounders: \[\text{logit}(P(y=1|t,z)) = \beta_0 + \beta_t t + \beta_z z\]

  • then the ATE is not equal to \(\beta_t\) anymore, but can be computed from the regression model: \[\begin{align} \text{ATE} &= E[Y|\text{do}(t=1)] - E[Y|\text{do}(t=0)] \\ &= E_z[P(y=1|t=1,z)] - E_z[P(y=1|t=0,z)] \\ &= E_z[\text{logit}^{-1}(\beta_0 + \beta_t * 1 + \beta_z z)] - E_z[\text{logit}^{-1}(\beta_0 + \beta_t * 0 + \beta_z z)] \end{align}\]

  • after fitting a logistic regression model in R with glm, the ATE can be computed with the package marginaleffects (or margins)

General estimators for the ATE and the CATE (meta-learners)

  • denote \(\tau(w) = E[y|\text{do}(t=1),w] - E[y|\text{do}(t=0),w]\)
    • (assuming \(W\) is a sufficient set)
  • T-learner: model \(T=0\) and \(T=1\) separately (e.g. regression separetely for treated and untreated): \[\begin{align} \mu_0(w) &= E[Y|\text{do}(T=0),W=w] \\ \mu_1(w) &= E[Y|\text{do}(T=1),W=w] \\ \tau(w) &= \mu_1(w) - \mu_0(w) \end{align}\]
  • S-learner: use \(T\) as just another feature \[\begin{align} \mu(t,w) &= E[Y|T=t,W=w] \\ \tau(w) &= \mu(1,w) - \mu(0,w) \end{align}\]
  • (many other variants combinations: this is a whole literature)

Doubly robust estimators

  • In day 1, we saw that the ATE can be estimated with the propensity score:

\[e(w) = P(T=1|W=w)\]

  • Doubly robust estimators combine the propensity score and outcome regression:

\[\begin{align} \hat{\tau}_{DR} &= \frac{1}{n} \sum_{i=1}^n \left[ \frac{T_i Y_i}{\hat{e}(W_i)} - \frac{(1-T_i) Y_i}{1-\hat{e}(W_i)} + \hat{\mu_1}(W_i) - \hat{\mu_0}(W_i) \right] \end{align}\]

  • They have the property that if either the propensity score model or the outcome regression model is correctly specified, the estimator is consistent for the ATE.
  • In addition, they may be more efficient than either method alone, especially when both models are correctly specified.

How to choose between estimators?

Intuitive way-pointers:

  • where does the complexity come from?
    1. variance in outcome under control: \(E[y|\text{do}(T=0),w]\)
    2. variance CATE: \(\tau(w)\) (in statistics: interaction between treatment and covariate)

Where does the variance come from?

DAG
Figure 1: Three datasets with the same DAG
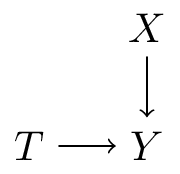
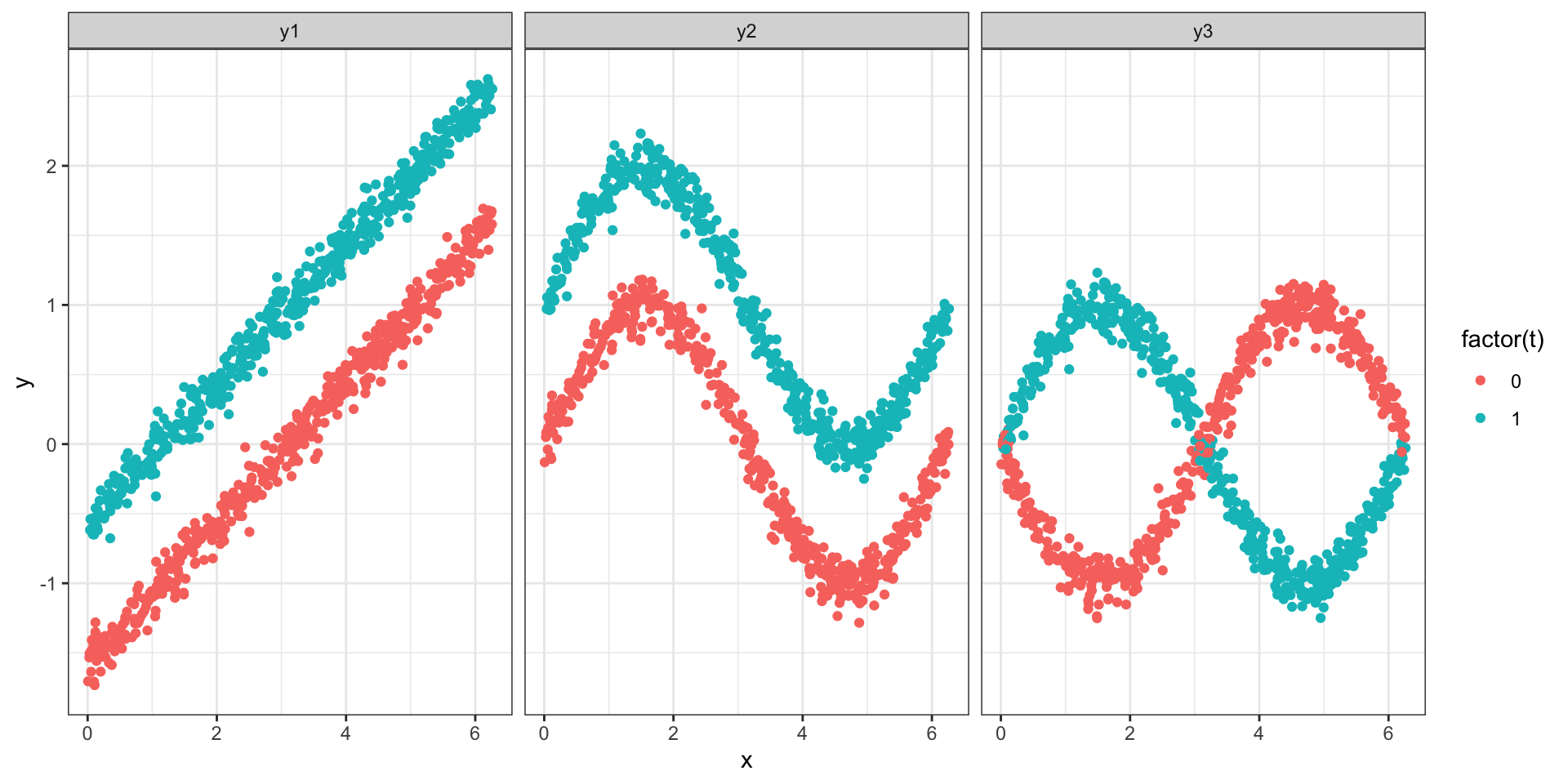
  1. \(Y = T + 0.5 (X - \pi) + \epsilon\) (linear)
  2. \(Y = T + \sin(X) + \epsilon\) (non-linear additive)
  3. \(Y = T * \sin(X) - (1-T) \sin(x) + \epsilon\) (non-linear + interaction)

Limitations of DAGs and SCMs

Making DAGs

  • how do you get a DAG? up to now we assumed we had one
  • based on prior evidence, expert knowledge
  • “no causes in, no causes out”

A003024: The death of DAGs?

The number of possible DAGs grows super-exponentially in the number of nodes

n_nodes n_dags time at 1 sec / DAG
1 1
2 3
3 25
4 543
5 29281 > an hour
6 3781503 > a day
7 1138779265 > a year
8 783702329343
9 1213442454842881 > human species
10 4175098976430598143 > age of universe

Do we need to consider all DAGs?

  • a single sufficient set suffices
  • adjusting for all direct causes of the treatment or all direct causes of the outcome are always sufficent sets
  • can we judge these without specifying all covariate-covariate relationships?
  • potential approach:
    • put all potential confounders in a cluster (e.g Anand et al. 2023)
    • ignore covariate-covariate relationships in that cluster
    • what happens when (partial) missing data?

SCM vs potential outcomes

  • definition of causal effect
    • PO: averages of individual potential outcomes
    • SCM: submodel or mutilated DAG
  • both require positivity
  • d-separation implies conditional independence (exchangeability)

References

Anand, Tara V., Adele H. Ribeiro, Jin Tian, and Elias Bareinboim. 2023. “Causal Effect Identification in Cluster DAGs.” Proceedings of the AAAI Conference on Artificial Intelligence 37 (10): 12172–79. https://doi.org/10.1609/aaai.v37i10.26435.